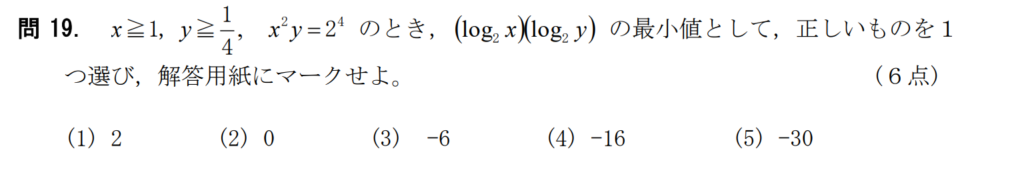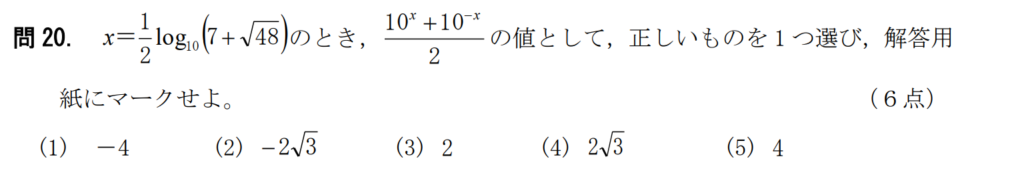航空大学校過去問【2015年度(H27)　総合Ⅱ　解答・解説】

Jです。

航空大学校過去問解説です。

他の年度の過去問解説もありますのでブログの「航空大学校過去問解説」からチェックしてみてください。

毎年同じような問題なので傾向と対策は立てやすいかと思います。

 

でも、ただ解くだけではなく、できるだけ最短の解き方をしています。

僕の解説のように解けば余った時間を他の問題に回すことができると思います。

問１【時事問題：航空知識】答え③

航空大学校HPより引用

LCCは”Low Cost Carrier”の略。今では当たり前だが、当時は画期的だった。

問２【時事問題】答え③

航空大学校HPより引用

領海は沿岸から12海里なので(3)は間違い。

問３【社会：社会問題】答え②

航空大学校HPより引用

この「内容が正しいものは何個あるか問題」は全部の選択肢の〇×が分からないと解けないので1番タチが悪い。

問４【社会：文化系の知識】答え②

航空大学校HPより引用

この「内容が正しいものは何個あるか問題」は全部の選択肢の〇×が分からないと解けないので1番タチが悪い。

この年度は多いな。

問５【地学：地球温暖化】全員正解として処理

航空大学校HPより引用

たまに出る全員正解問題。

こういうことがあるので分からない問題は後回しにして先に解けるものから解きましょう。

地球温暖化は頻出分野。

問６【化学：天気図】答え⑤

航空大学校HPより引用

 

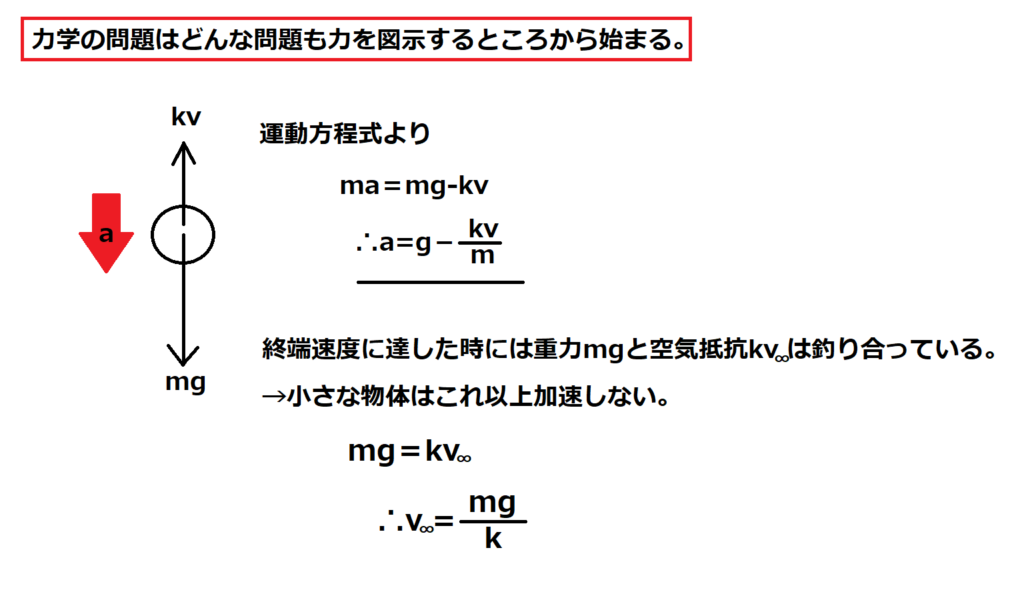
問７【物理：運動方程式】答え(a)⑤.(b)④

航空大学校HPより引用

問８【物理：気体】答え④

航空大学校HPより引用

問題文をいかに正しく読めるかが鍵。

聞き方をややこしくしている。

聞き方がややこしいがこの問題文は以下のように言い換えることができる。

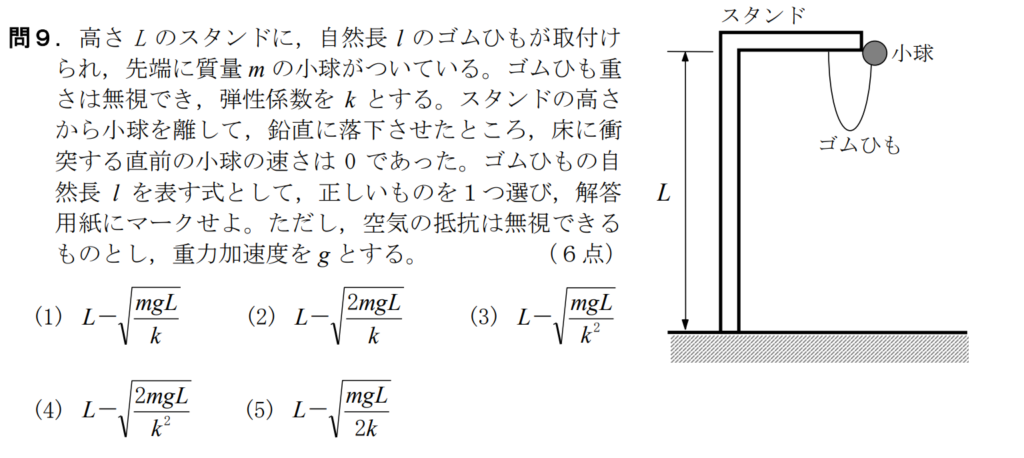
問９【物理：エネルギー保存則】答え②

航空大学校HPより引用

問１０【物理：円運動】答え⑤

航空大学校HPより引用

まずは円運動とは何かを押さえること。

物体の進行方向と垂直の向きに一定の力が働いた時に円運動となり、その力と加速度はその円の中心に向かって働く。

この問題の場合、円の中心方向に働いている力というのは摩擦力のことである。

摩擦力が無ければ円運動は成立しない。

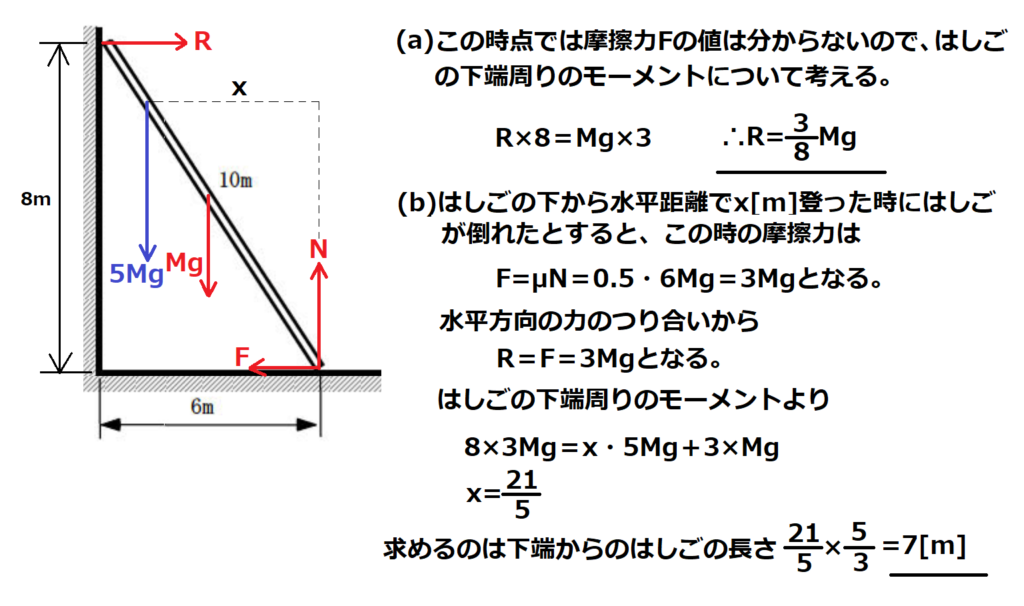
問１１【物理：力のモーメント】答え(a)①.(b)①

航空大学校HPより引用

問題文のはじめにしれっと書いている「滑らかな鉛直壁から・・・」の「滑らか」という一言が超重要。

物理において「滑らか」というのは「摩擦がない」ということを意味している。

よってはしごが壁から受ける力は垂直抗力のみである。

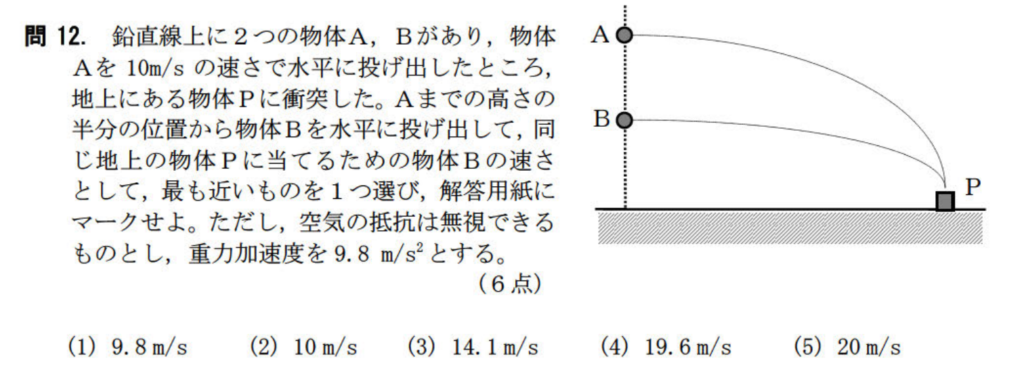
問１２【物理：等加速度直線運動】答え③

航空大学校HPより引用

解き方はいろいろあるので試行錯誤したらいいと思う。

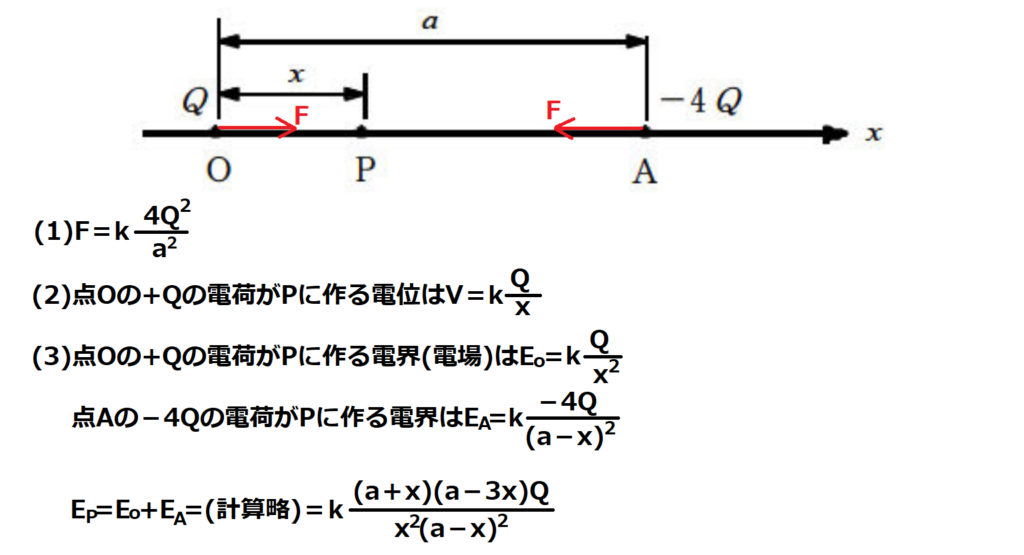
問１３【物理：クーロン力】答え⑤

航空大学校HPより引用

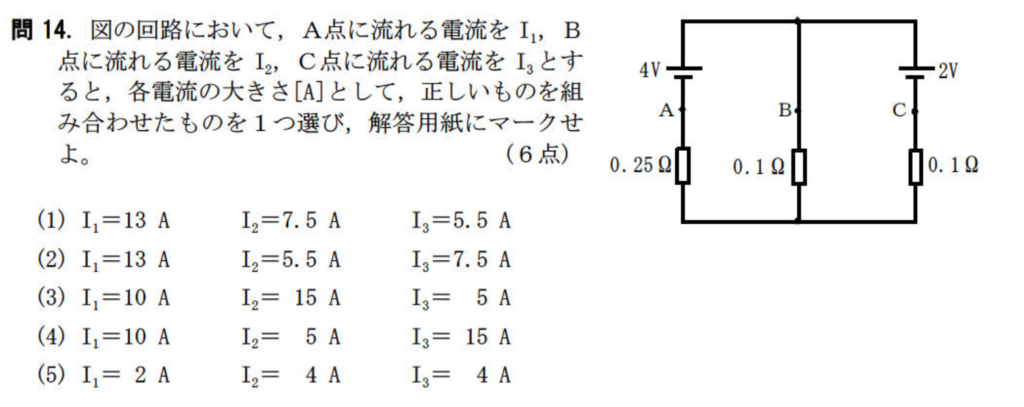
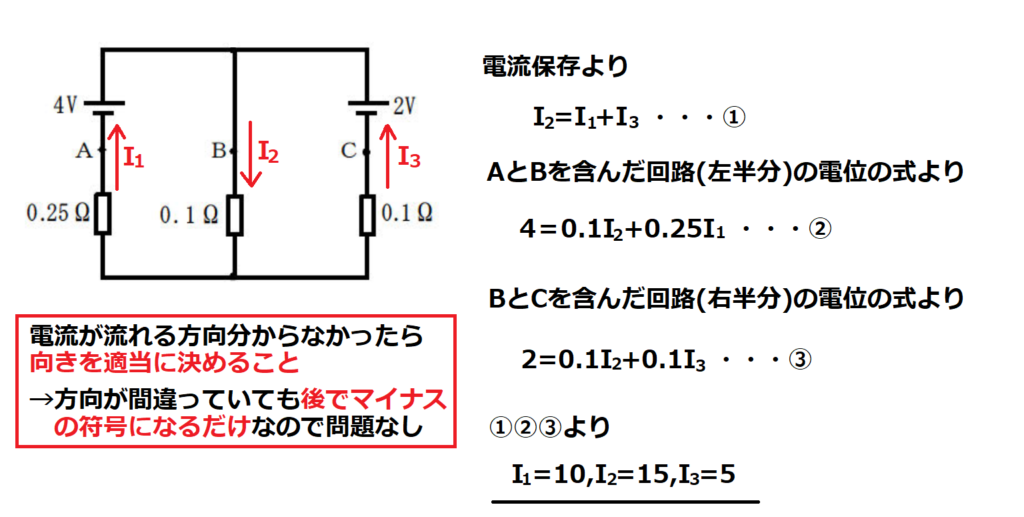
問１４【物理：電気回路】答え③

航空大学校HPより引用

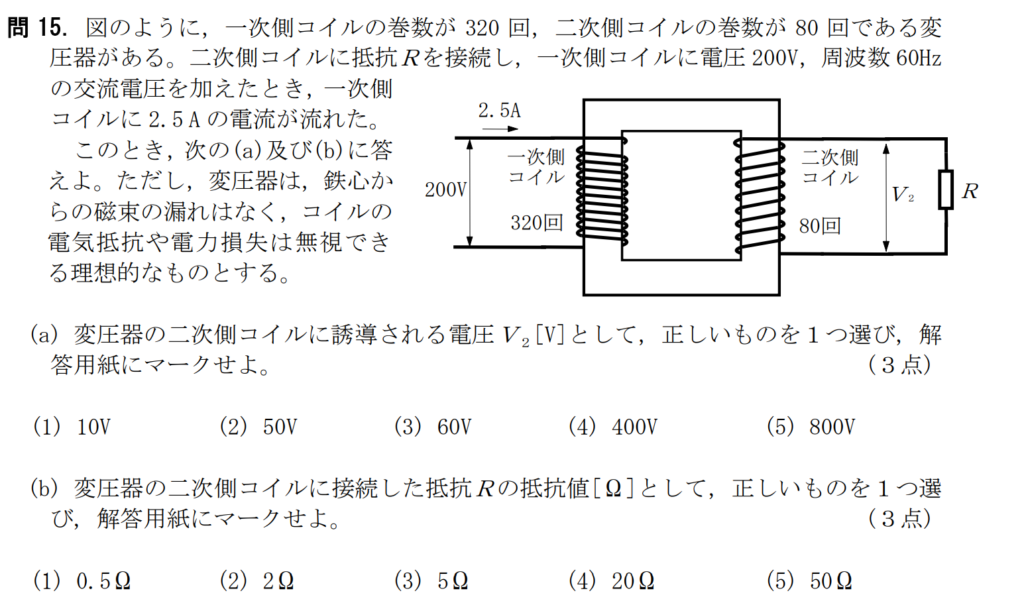
問１５【物理：電磁誘導】答え(a)②.(b)③

航空大学校HPより引用

問１６【数学：場合の数】答え②

航空大学校HPより引用

配る人数をx人、ボールの数をy個と置く。(y≧40)

 

6個配ると11個余るので、等式”6x+11＝y”・・・①が成り立つ。

8個ずつ配ると余るとのことなので不等式”8x<y“・・・②が成り立つ。

9個ずつ配ると不足するので不等式”9x>y“・・・③が成り立つ。

 

①②③より”8x<6x+11<9x”でこれを解くと3.66<x<5.5となる。

よってxの値は4か5となる。

x=4のとき①の式よりy=35となり、これはy≧40を満たさない。

x=5のとき①の式よりy=41となり、これはy≧40を満たす。

よって41個

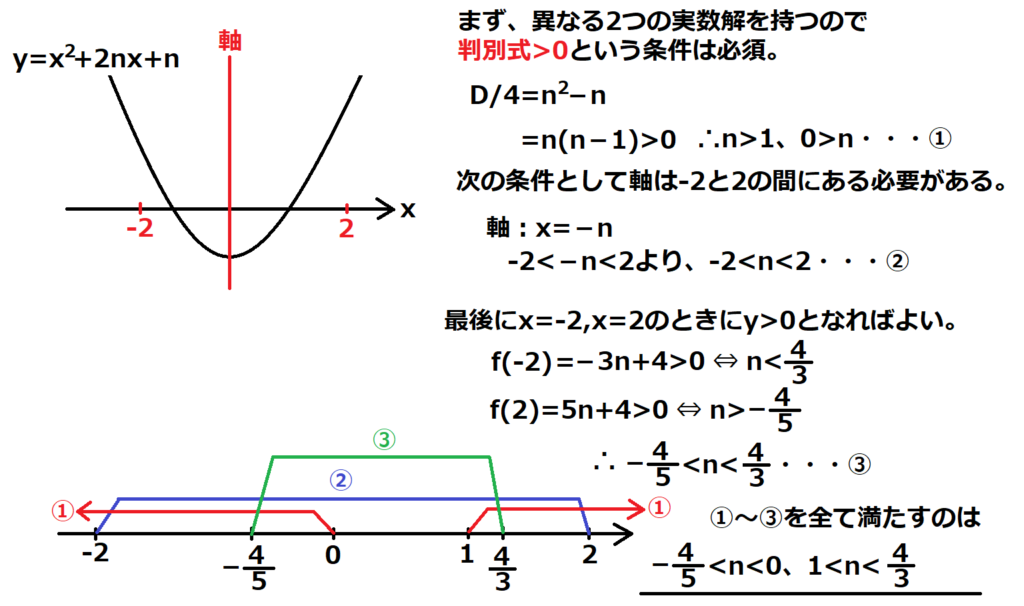
問１７【数学：2次方程式】答え④

航空大学校HPより引用

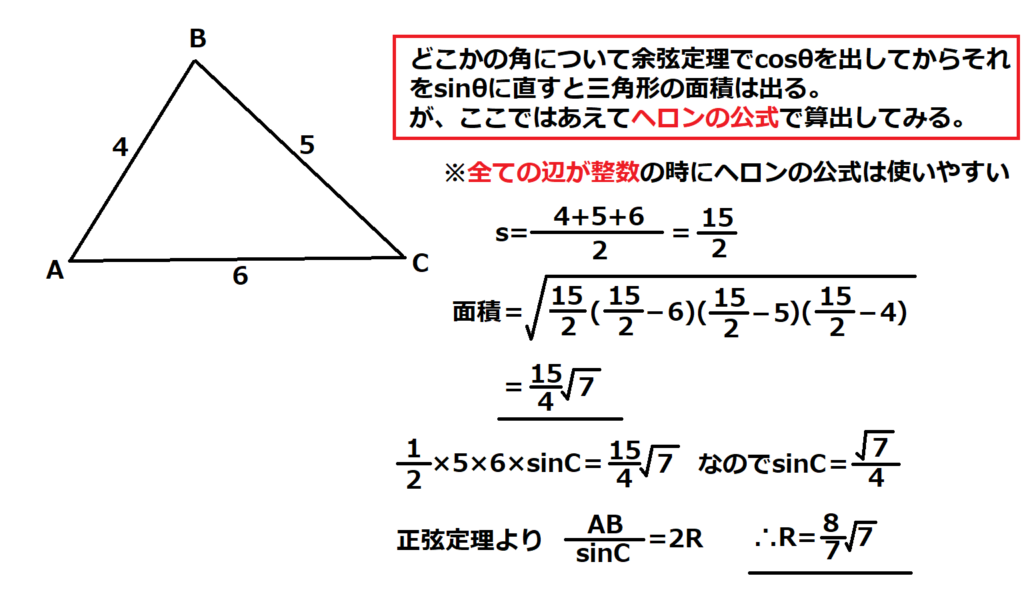
問１８【数学：図形】答え(a)②.(b)④

航空大学校HPより引用

問１９【数学：対数関数】答え③

航空大学校HPより引用

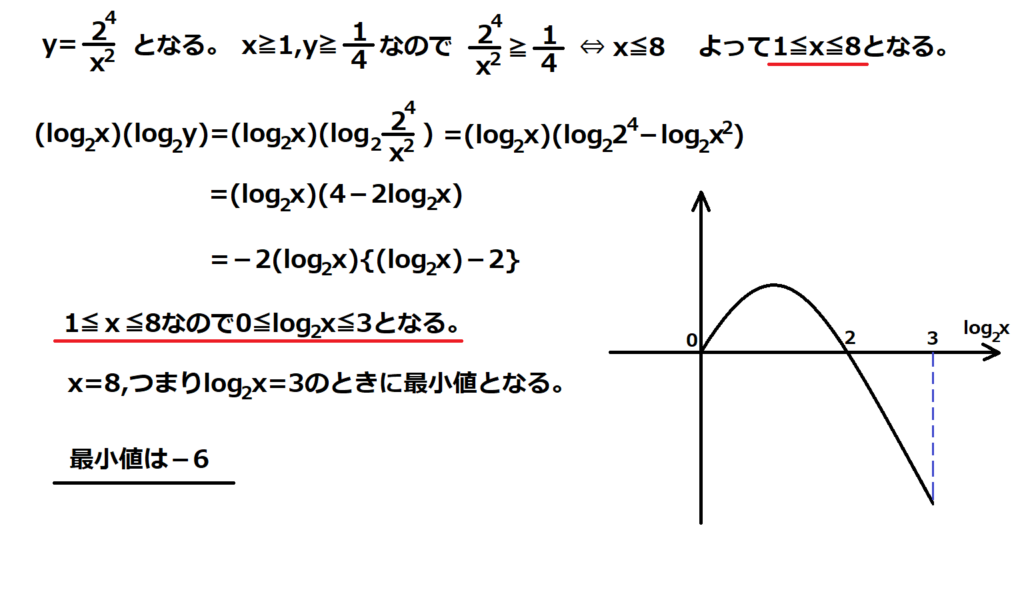
こういう問題はxやyの範囲が超重要。

x²y=24の両辺をx²で割る。(x≧1なので割ってよし)

問２０【数学：指数対数関数】答え③

航空大学校HPより引用

この問題で1番重要なのは「10^log₁₀a=a」ということである。

(証明)
10^log₁₀a=yと置き、両辺log₁₀を取る。
log₁₀10^log₁₀a=log₁₀y
⇔log₁₀a=log₁₀y
⇔a=y
よって10^log₁₀a=y=a

 

問２１【数学：図形】答え④

航空大学校HPより引用

「方べきの定理」を知っているかどうかの問題。

PT²＝PA×PBが成り立つ。

よって5²＝3(3+x)

答えは(4)

問２２【数学：ベクトル】答え①

航空大学校HPより引用

問２３【数学：微分】答え④

航空大学校HPより引用

f(x)を微分する。

f'(x)＝6x²－6(a+1)x+6a=6(x－a)(x－1)

f'(x)＝0のときx=1、aとなる。

1≦aであり、xの範囲は0≦x≦1なので

増減表より、最大値はf(1)＝3a

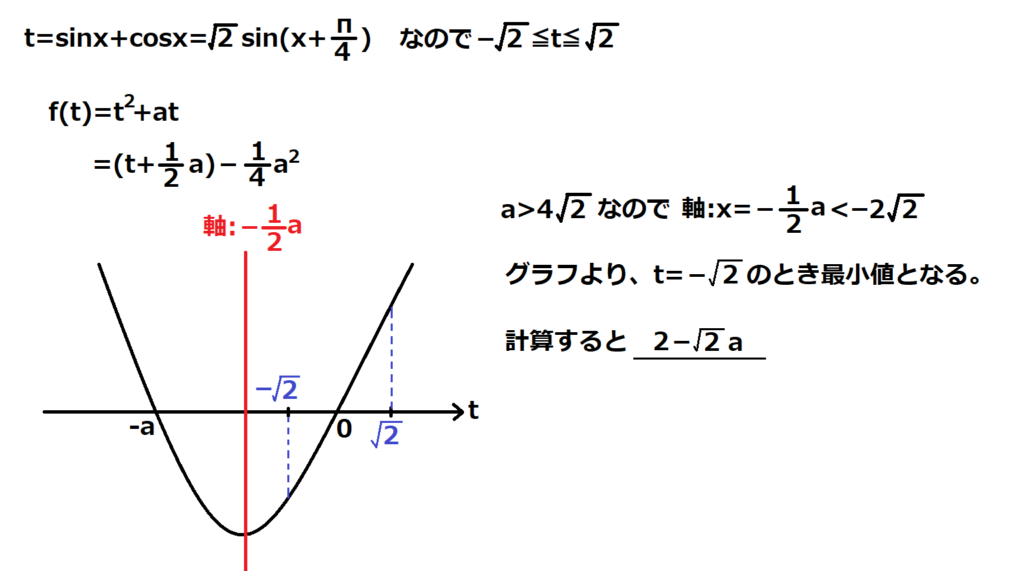
問２４【数学：三角関数】答え(a)②.(b)①

航空大学校HPより引用

(a)
sinx＋cosx=t の両辺を2乗する。(このやり方はワンパターン)

(sinx＋cosx)²＝t²
⇔sin²x+2sinxcosx+cos²x=t²
⇔1＋2sinxcosx＝t²
⇔2sinxcosx＝t²－1
⇔sin2x＝t²－1

よって
f(x)＝t²－1+at+1＝t²+at

(b)

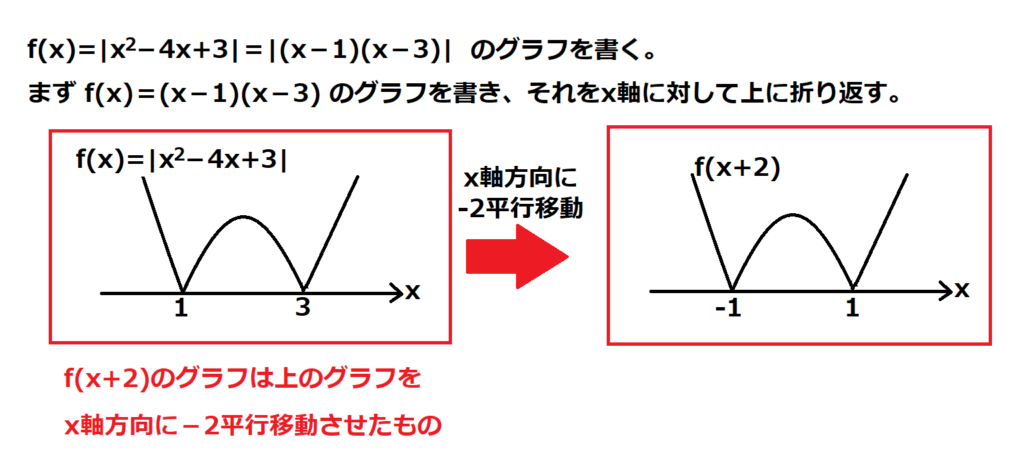
問２５【数学：積分】答え③

航空大学校HPより引用

絶対値を含んだ積分問題はよく出る。

航空大学校過去問【2016年度(H28)　総合Ⅱ　解答・解説】