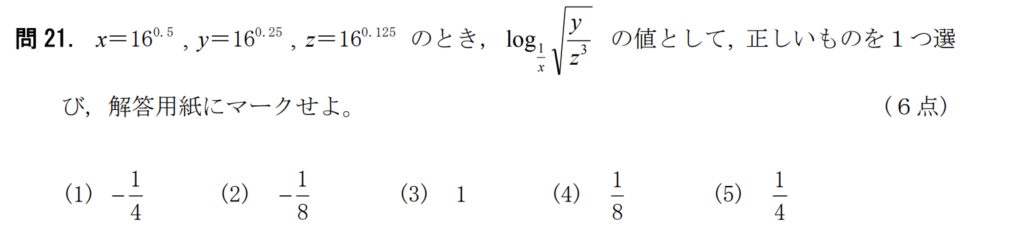航空大学校過去問解説です。
他の年度の過去問解説もありますのでブログの「航空大学校過去問解説」からチェックしてみてください。
毎年同じような問題なので傾向と対策は立てやすいかと思います。
でも、ただ解くだけではなく、できるだけ最短の解き方をしています。
僕の解説のように解けば余った時間を他の問題に回すことができると思います。
目次
問1【時事問題:航空系】答え④
航空大学校HPより引用
問2【時事問題】答え②
航空大学校HPより引用
こういうのが1番難しかったりする。
問3【時事問題】答え④
航空大学校HPより引用
問4【時事問題】答え⑤
航空大学校HPより引用
問5【化学】答え③
航空大学校HPより引用
(イ)のイタイイタイ病の原因物質は「カドミウム」なのでこの選択肢は間違い。
一般常識として四大公害病について復習しておきましょう。
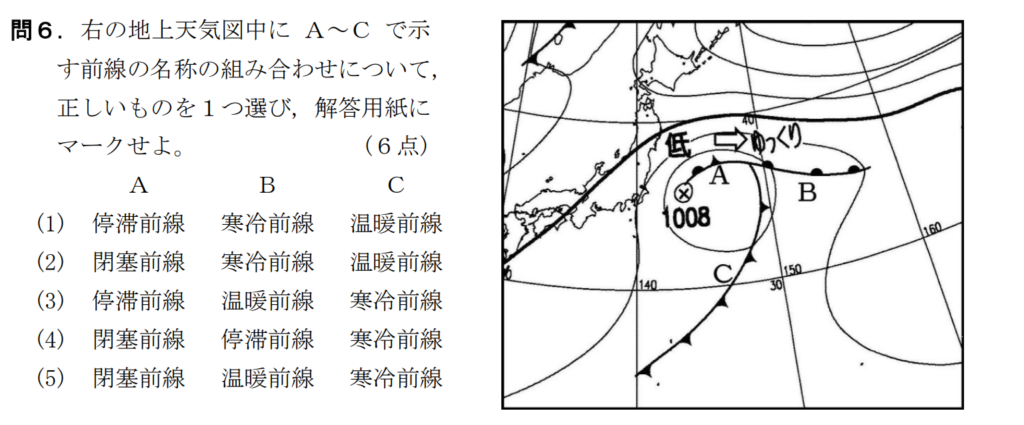
問6【地学:天気図】答え⑤
航空大学校HPより引用
知っているか知っていないか。
この知識はパイロットとして基礎の基礎なので覚えましょう。
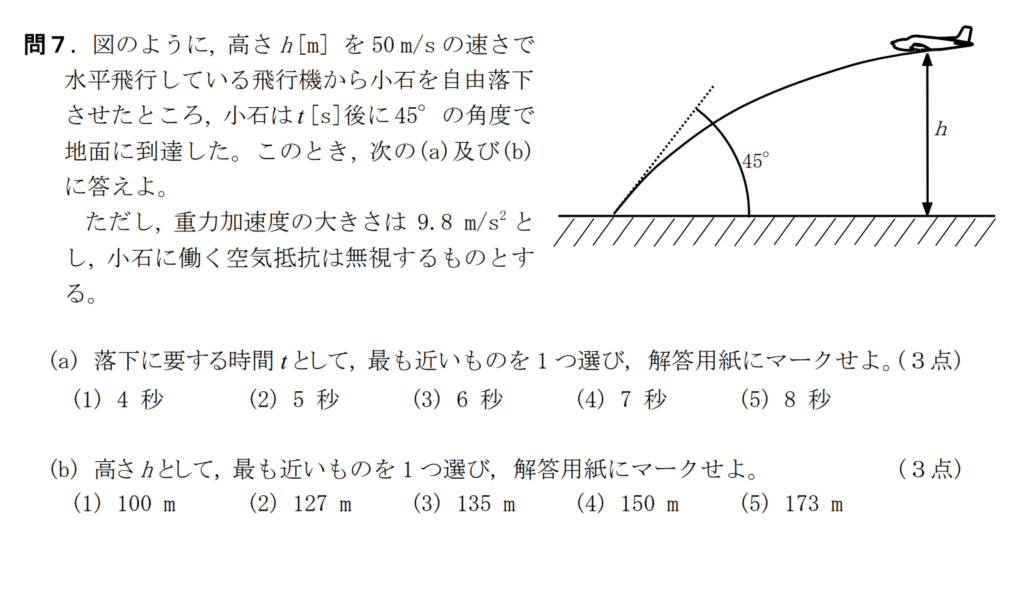
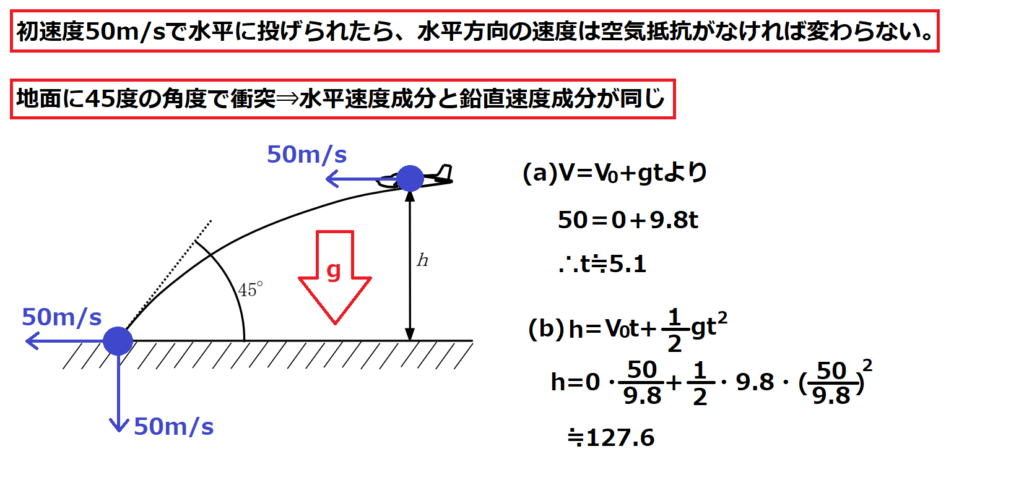
問7【物理:等加速度直線運動】答え(a)②.(b)②
航空大学校HPより引用
与えられた情報がどういう意味なのかしっかり読み替える。
問8【物理:等加速度直線運動】答え②
航空大学校HPより引用
放物線を描いて水平方向の速度が一定の運動をするとき、垂直方向の運動は等加速度直線運動である。
よってt秒後に8m/sであれば2t秒後は16m/s。
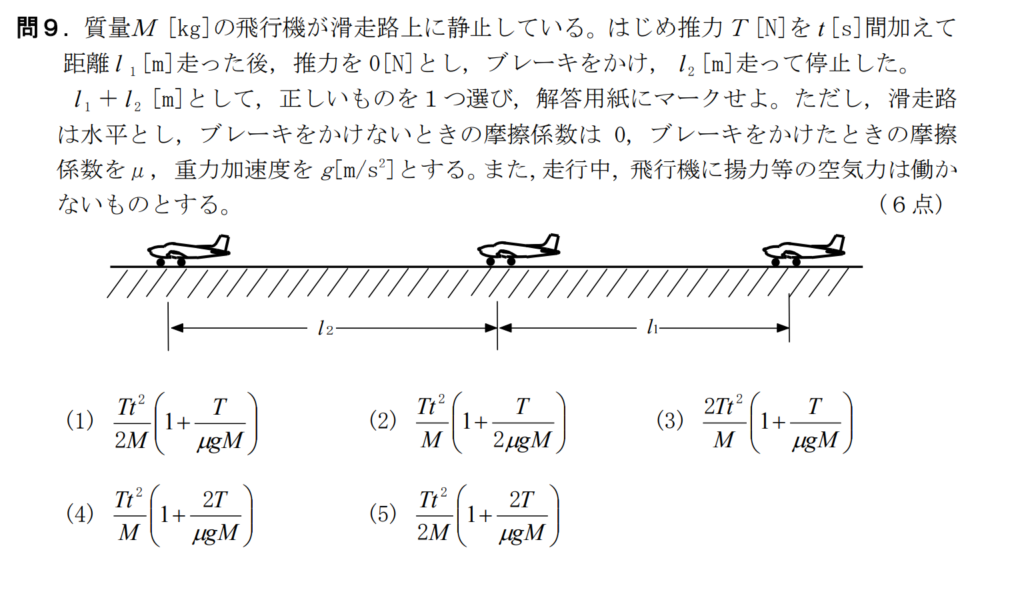
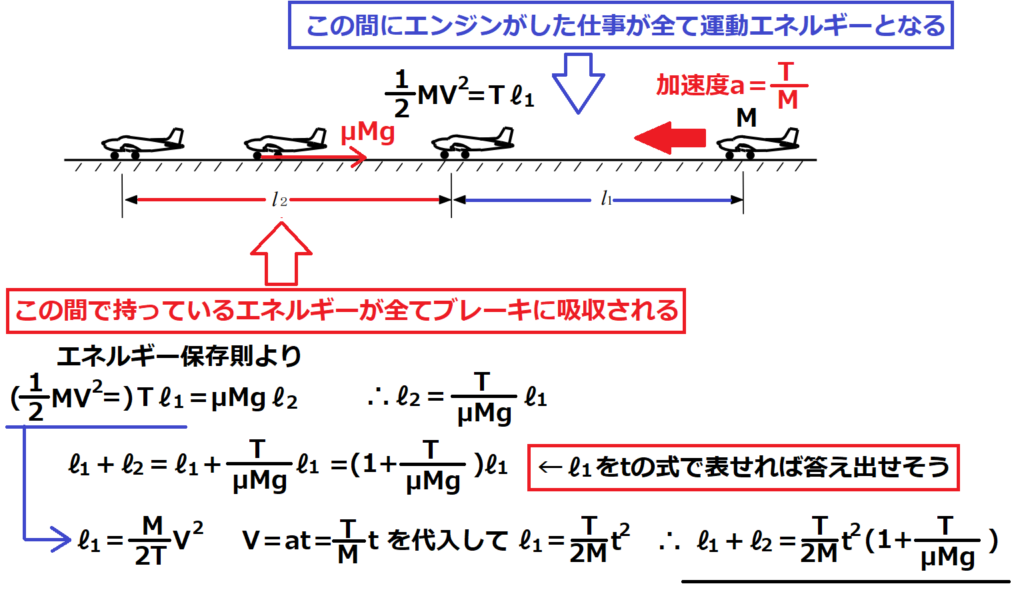
問9【物理:エネルギー保存則】答え①
航空大学校HPより引用
飛行機の離陸滑走中のエンジン故障をモデルにした問題。
問10【物理:エネルギー保存則】答え⑤
航空大学校HPより引用
衝突した時の運動エネルギーは元々は位置エネルギーである。
エネルギーは「位置エネルギー→運動エネルギー→熱エネルギー」の順に変わっていて、そのエネルギーは保存されるという設定なので(普通は保存されないが)
熱エネルギー=mgh=2[kg]×9.8×10[m]=196[J]
問11【物理:ドップラー効果】答え(a)②.(b)①
航空大学校HPより引用
他の年度の解説でも言っているが、「ドップラー効果の式は覚えてはいけない」。
式の丸覚えで解けるのは典型的な簡単な問題くらいなので、まずは現象の正確な理解が大事。
そもそもドップラー効果とは何なのか、振動数[Hz]とは、波長λとは、波の基本式v=fλのことを正確に理解するのが大事。
ちなみに音叉は「おんさ」と読む。(今知った)
(a)
「うなり」とは2つの振動数の近い音を同時に聞いた時に起こる現象。2つの音の振動数の差がうなりの振動数となる。
よって答えは20Hz。
(b)
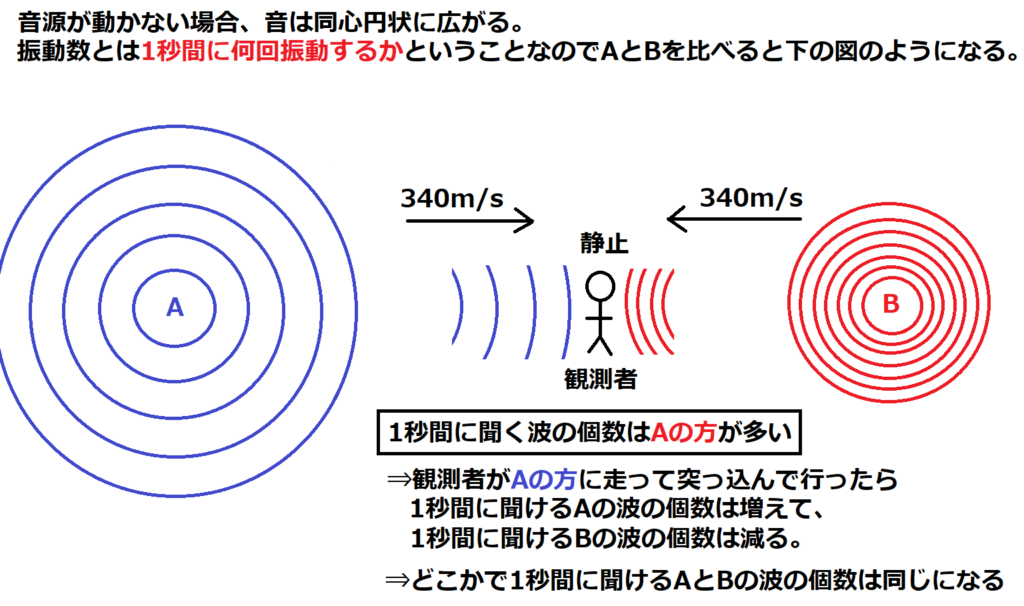
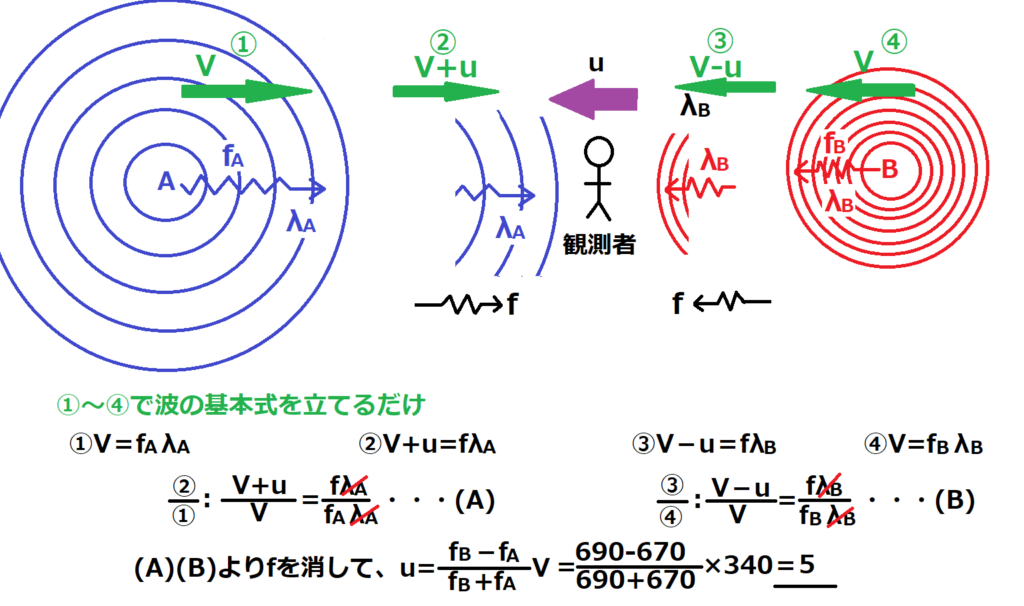
うなりが聞こえないということはAとBから観測者が聞く振動数が同じになったということである。
670Hzと690Hzの2つの振動数の間で観測者が動くことでドップラー効果が生じ、動く速度がある値の時には結果としてAとBの振動数が同じに聞こえるということ。
振動数とは何かを正しく理解していれば式を立てなくともどっちに動いたかは瞬時に分かる。
Aの方向に動いた方が青の波に向かっていくわけなので青の波とぶつかる回数が多くなり、赤の波からは逃げていくわけなので赤の波とぶつかる回数は減るのが分かる。
ぶつかる回数が多くなるというのは観測する振動数が大きくなるということで、ぶつかる回数が減るということは観測する振動数が小さくなるということである。
これをドップラー効果という。
この定性的な理解が大事。公式はゴミ箱へ捨てましょう。
その時点で答えは①③⑤の3択。
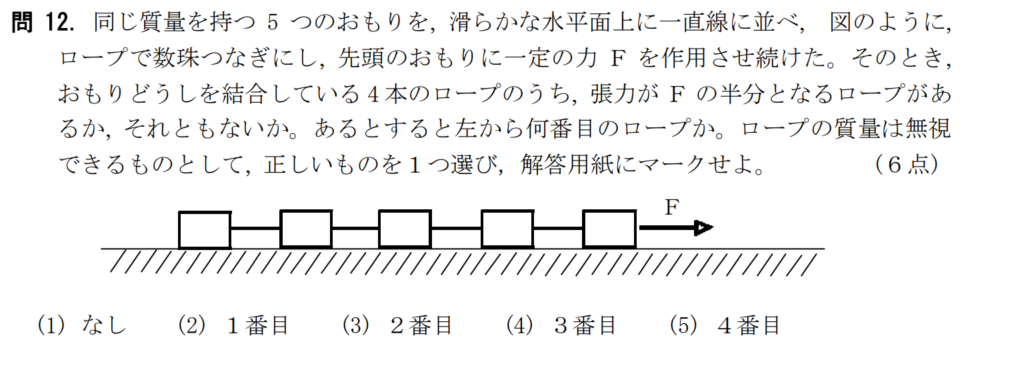
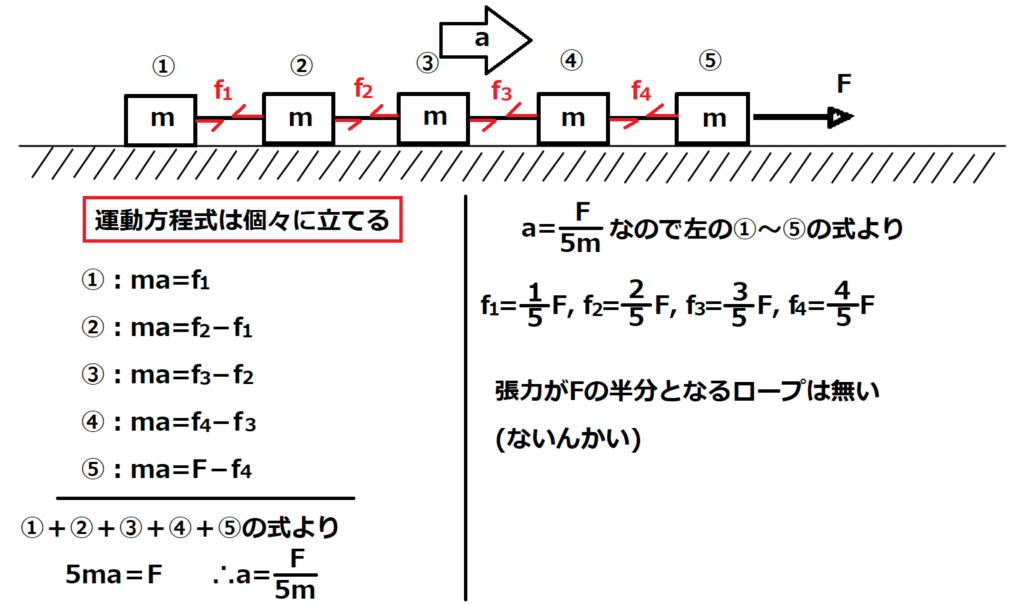
問12【物理:運動方程式】答え①
航空大学校HPより引用
他の問題でも散々言ってますが、もう1度言います。
運動方程式は個々の物体について立てること。
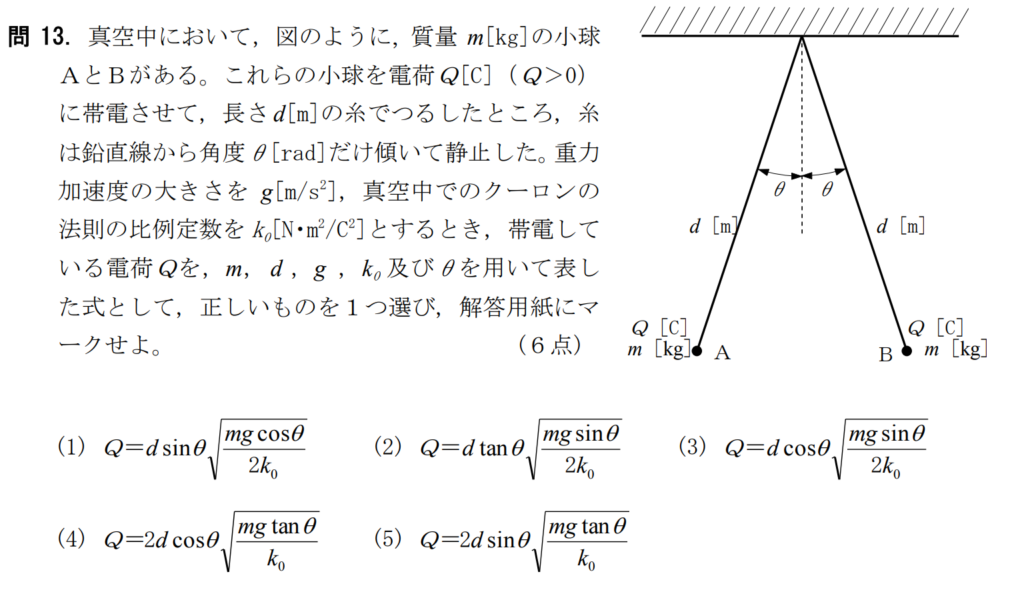
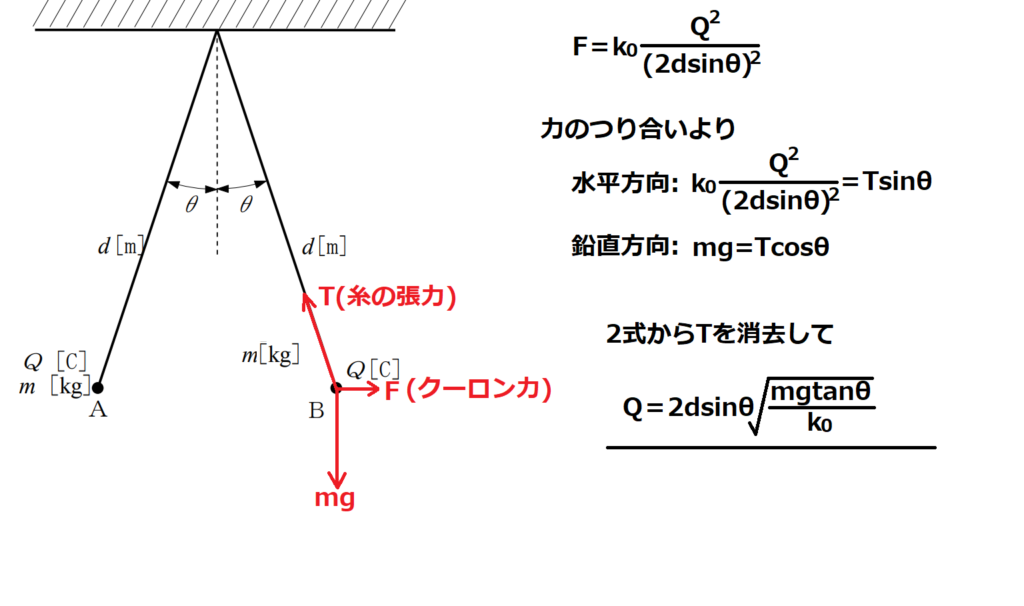
問13【物理:力のつり合い】答え⑤
航空大学校HPより引用
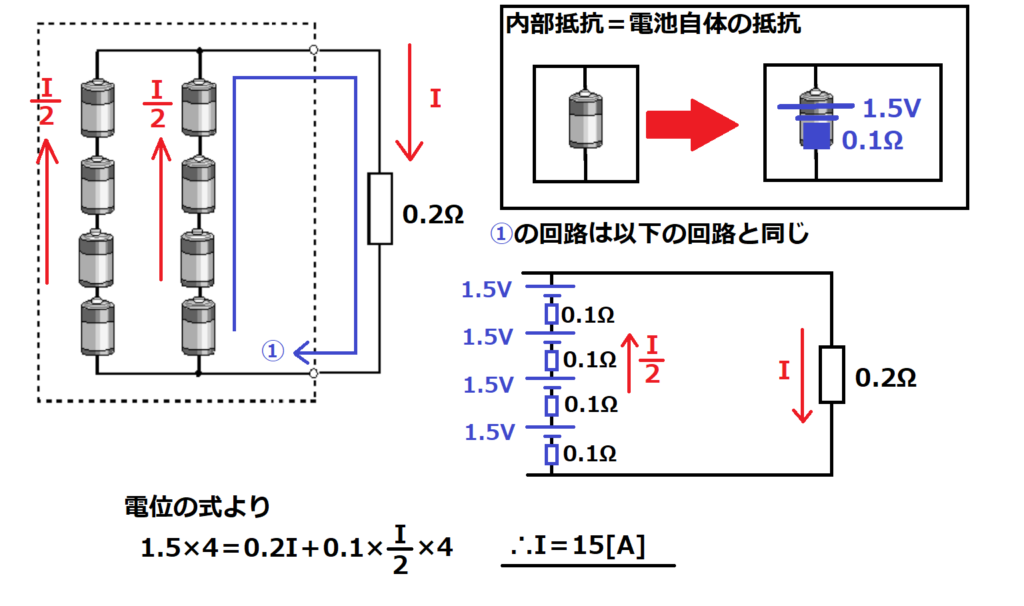
問14【物理:電気回路】答え③
航空大学校HPより引用
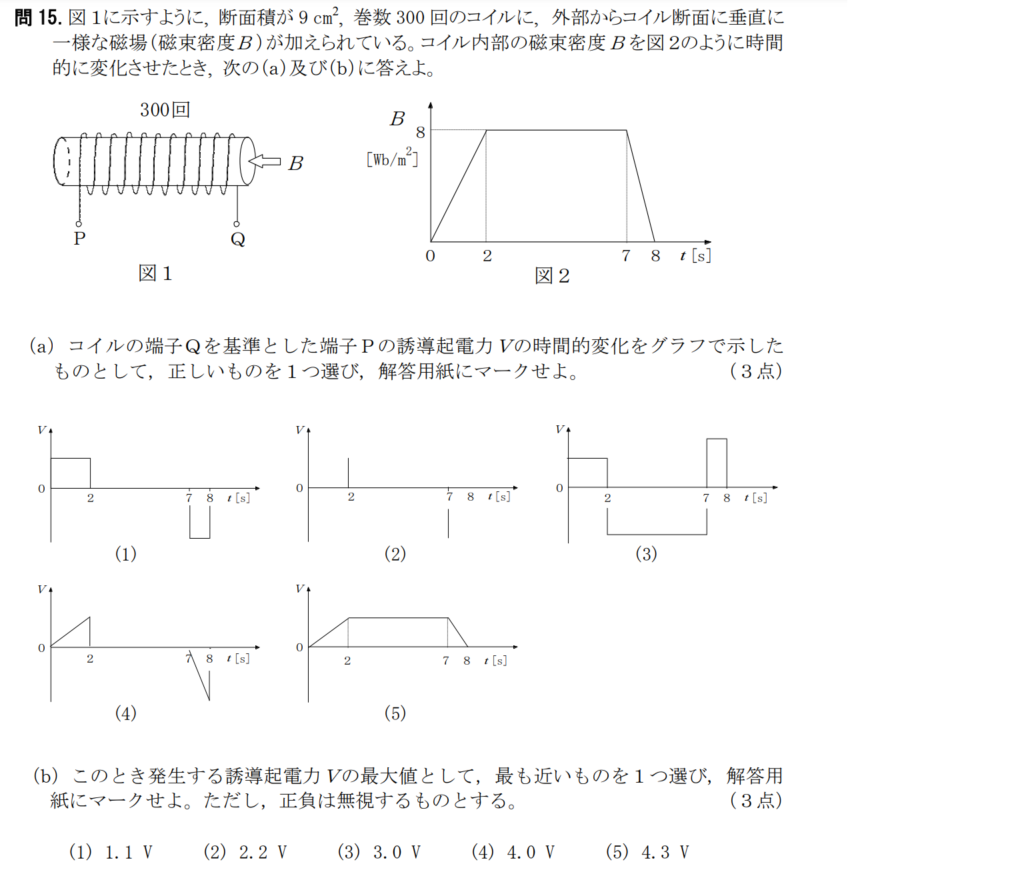
問15【物理:電磁誘導】答え(a)①.(b)②
航空大学校HPより引用
(a)
誘導起電力は磁場の変化があるときに発生する。
よって0~2秒のところと7~8秒のところで誘導起電力は発生し、2~7秒のところでは誘導起電力は発生しない。
また、誘導起電力は磁場の時間変化率が同じであれば一定値となる。(下のファラデーの法則参照)
よってグラフ(1)が正しい。
問16【数学:因数分解】答え①
航空大学校HPより引用
この問題は最悪選択肢をひとつひとつ展開していければ解ける。
こういうタイプの問題はどれか1つの文字についての方程式だと思って並べるところから始まる。
ここではxの多項式として整理する。
3x2+2y2-3z2-7xy-yz+8zx=3x2+(8z-7y)x+2y2-3z2-yz
因数分解できるということはxに関係のない「2y2-3z2-yz」の部分は必ず掛け算の形に変形できる。
3x2+(8z-7y)x+2y2-3z2-yz=3x2+(8z-7y)x+(2y-3z)(y+z)
=(3x-y-z)(x-2y+3z)・・・答え(1)
問17【数学:2次方程式】答え①
航空大学校HPより引用
この問題は選択肢がある故に瞬殺問題。
解と係数の関係を使う。
求める解xをα、βと置く。
もし本番にこういう問題が出たらこうやって解くと時間がかからない。
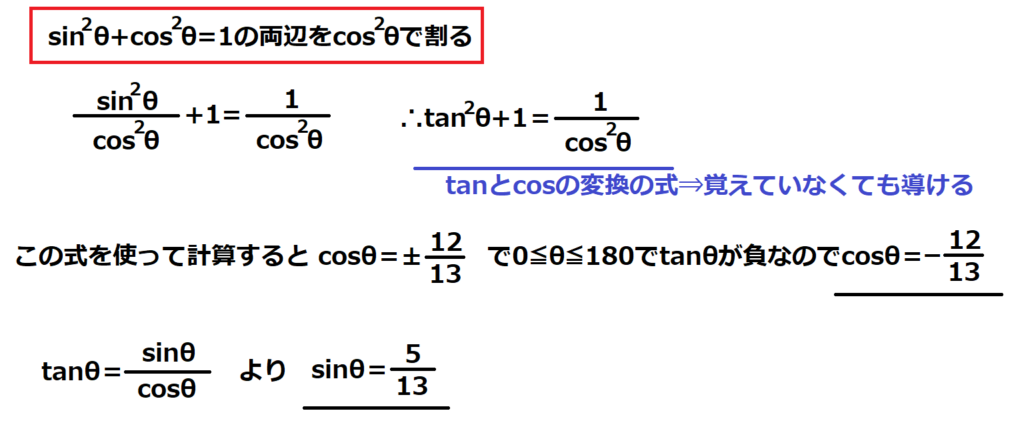
問18【数学:三角関数】答え(a)①.(b)③
航空大学校HPより引用
ただの計算問題。
問19【数学:三角関数】答え⑤
航空大学校HPより引用
直線の傾きはtanθで表せる。
よってy=-2x、y=3xのx軸とのなす角をそれぞれα、βと置くと、tanα=-2、tanβ=3となる。
2つの直線のなす角θはθ=α-βなので、tanの加法定理を用いて計算できる。
2020年度の解説ではベクトルを用いた解法をしているのでよかったらそちらも参考にしてください。
問20【数学:指数問題】答え④
航空大学校HPより引用
まずは普通に因数分解していく。
22x-2x-2<0 は (2x-2)(2x+1)<0と変形できる。
よって
-1<2x<2となるが2xは必ず正なので0<2x<2となる。
x=1を超えると2xは2より大きくなってしまうので、x<1となる。
問21【数学:指数対数関数】答え④
航空大学校HPより引用
・小数点は分数に直す
・ルートとは2分の1乗のこと
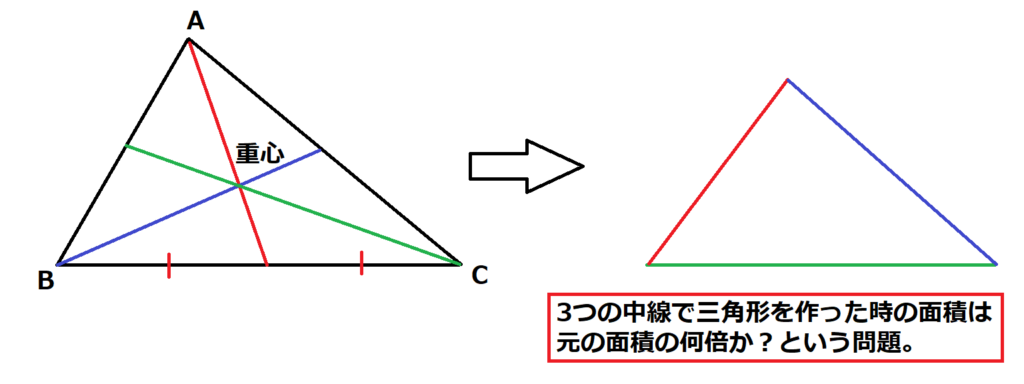
問22【数学:図形】答え③
航空大学校HPより引用
苦手な人は問題の意味がわからないのではないでしょうか。
そもそも「中線」って何だ?
三角形なんてできないんじゃ?
様々な疑問が沸いてきます。
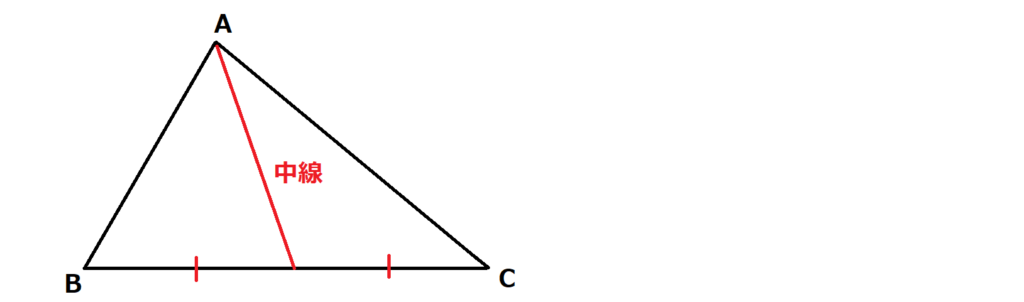
まず、押さえるべきは「中線」です。
三角形の1つの頂点から向かい合う辺の真ん中に引いた線分を「中線」といいます。
ちなみに三角形の3つの中線は1点で交わり、その点を三角形の重心と言います。
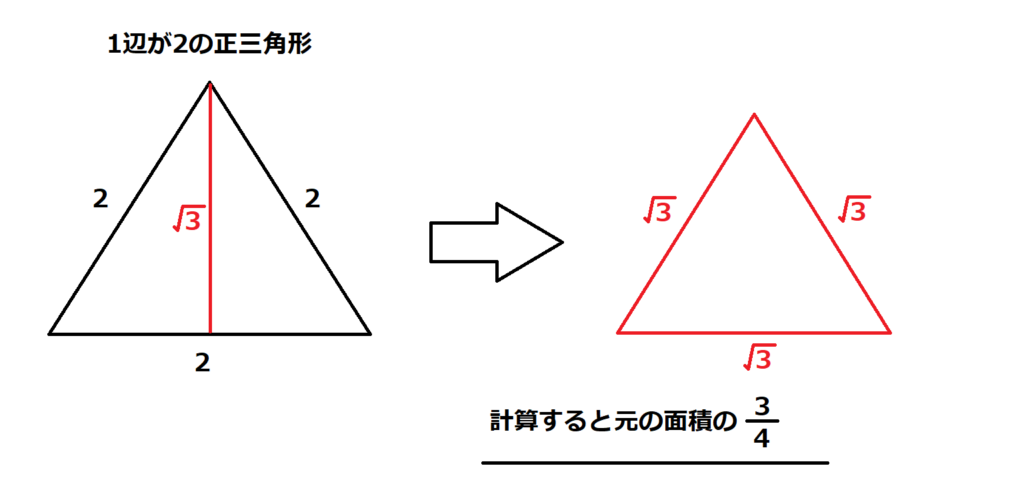
こういう一般的な問題は特定の条件の三角形で考えた方が分かりやすい。
→1辺2の正三角形で考える。
問23【数学:ベクトル】答え⑤
航空大学校HPより引用
「直交する」=「内積がゼロ」は合言葉。
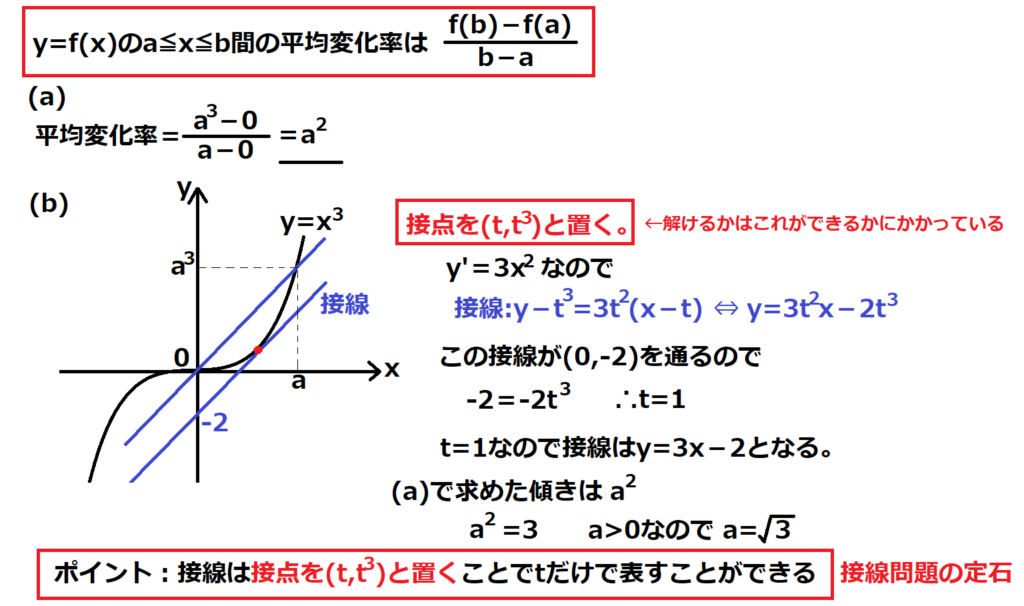
問24【数学:微分】答え(a)④.(b)④
航空大学校HPより引用
問25【数学:積分関数】答え①
航空大学校HPより引用
例えばx=2を代入すると、定積分を含んだ項は0になるのでf(2)=12になる。
その時点で選択肢の③と⑤は消える。
時間が無くて適当にマークする時に5択と3択では正答率が大きく違う。
時間が余った時の検算にも使える。マークシートの問題は部分点がない。
たとえ分かってなくても正解の答えをマークしたら勝ち。