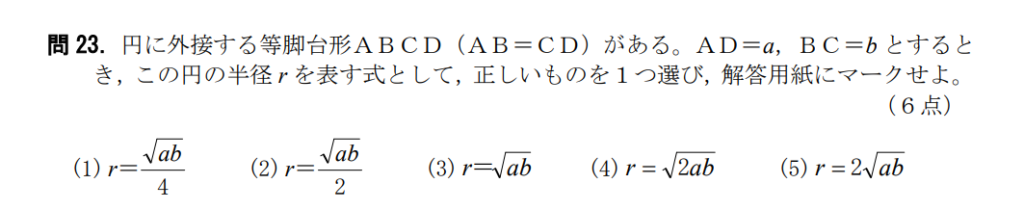航空大学校過去問【2020年度　総合Ⅱ　解答・解説】

Jです。

２０２０年度の総合問題Ⅱです。

他の年度の過去問解説もありますのでブログの「航空大学校過去問解説」からチェックしてみてください。

難易度は普通だと思います。

毎年同じような問題なので傾向と対策は立てやすいかと思います。

定員が増えてからは１次試験の倍率は３倍程度です。

 

でも、ただ解くだけではなく、できるだけ最短の解き方をしています。

僕の解説のように解けば余った時間を他の問題に回すことができると思います。

問１【時事問題：新政府専用機について】答え④

航空大学校HPより引用

 

問２【時事問題：新札の話】答え②

航空大学校HPより引用

その年に話題になったことに関しての時事問題。

新１万円札は渋沢栄一。新五千円札の裏は「ノダフジ」。新千円札は北里柴三郎。

 

問３【時事問題：新元号の話】答え①

航空大学校HPより引用

これもその年に話題になった時事問題。

問４【社会：法律】答え⑤

航空大学校HPより引用

(１)は「公務員」ってところが微妙。

(２)はわからず。

(３)みたいに選択肢が「～のみ」って書いてあるのは大体不正解。

(４)は明らかに言ってることおかしい。年功序列制度のことか。

以下調べた結果。

 

問５【社会：ヒートアイランド現象】答え⑤

航空大学校HPより引用

有名な問題。

ヒートアイランド現象は覚えておきましょう。

地球温暖化、大気汚染、エルニーニョ現象、ラニーニャ現象、オゾン層破壊も合わせて調べておくといいかも。

問６【物理：大気圏について】答え②

航空大学校HPより引用

(ア)(イ)が両方正しいので②。ちなみに(ウ)は間違いで、正しくは「オゾン層」。

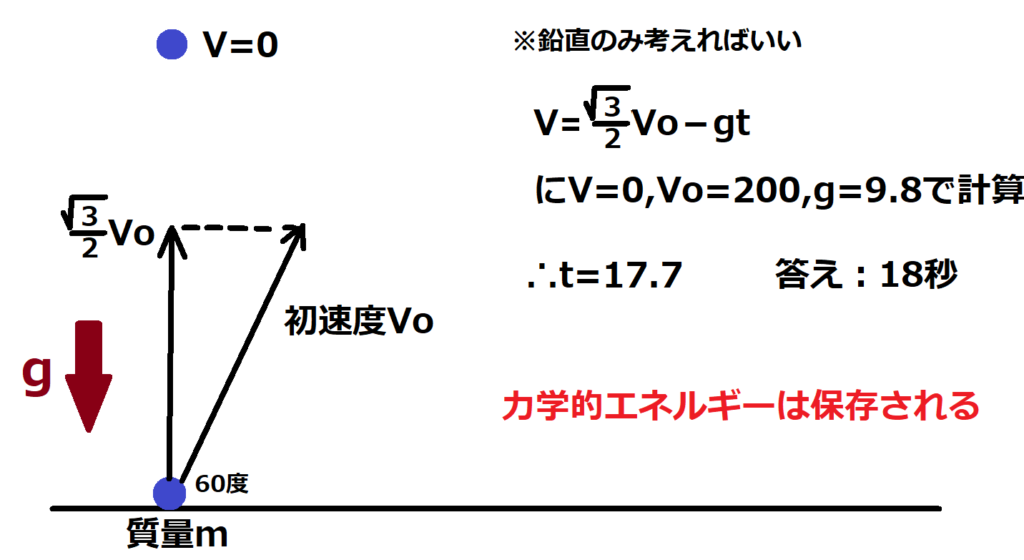
問７【物理：等加速度直線運動】a.④ b.③

航空大学校HPより引用

(a)重力は下向きなので「下向き加速度ｇの等加速度運動」

(b)

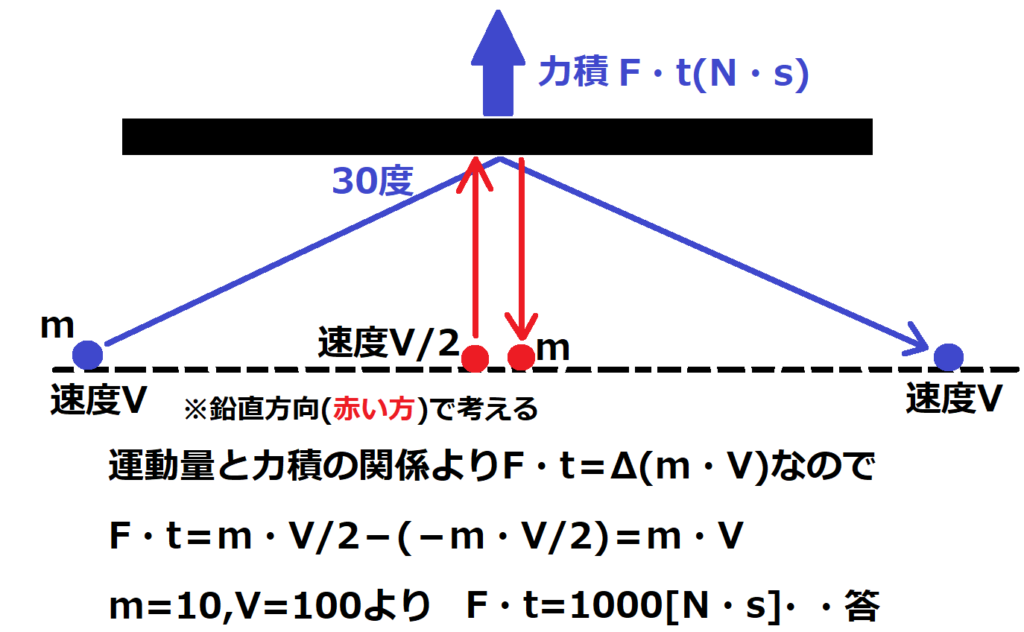
問８【物理：運動量と力積の関係】答え③

航空大学校HPより引用

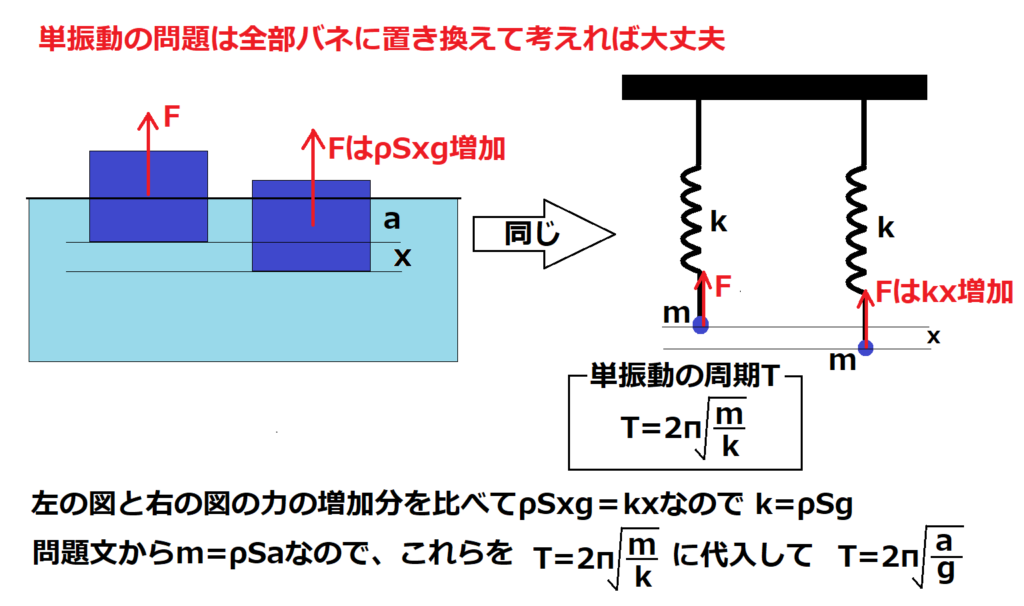
問９【物理：浮力、単振動】答え⑤

航空大学校HPより引用

瞬殺問題。単振動の周期の式は覚えておいて損はない。

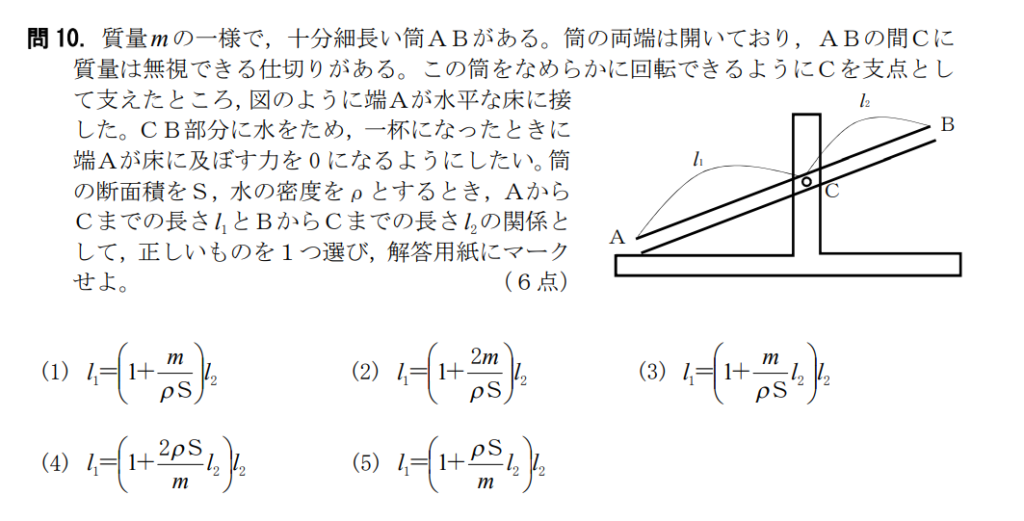
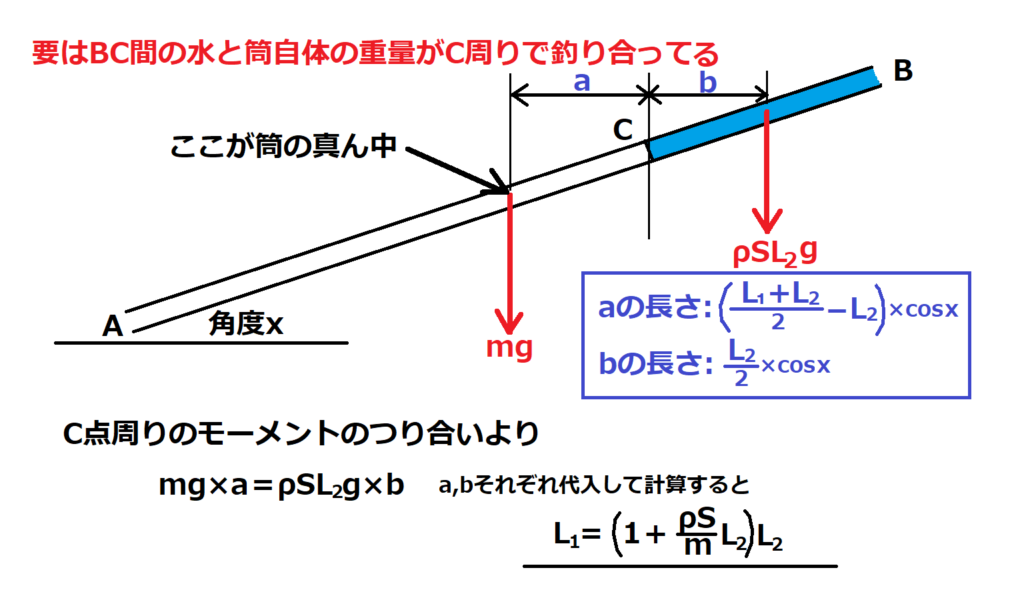
問１０【物理：力のモーメント】答え⑤

航空大学校HPより引用

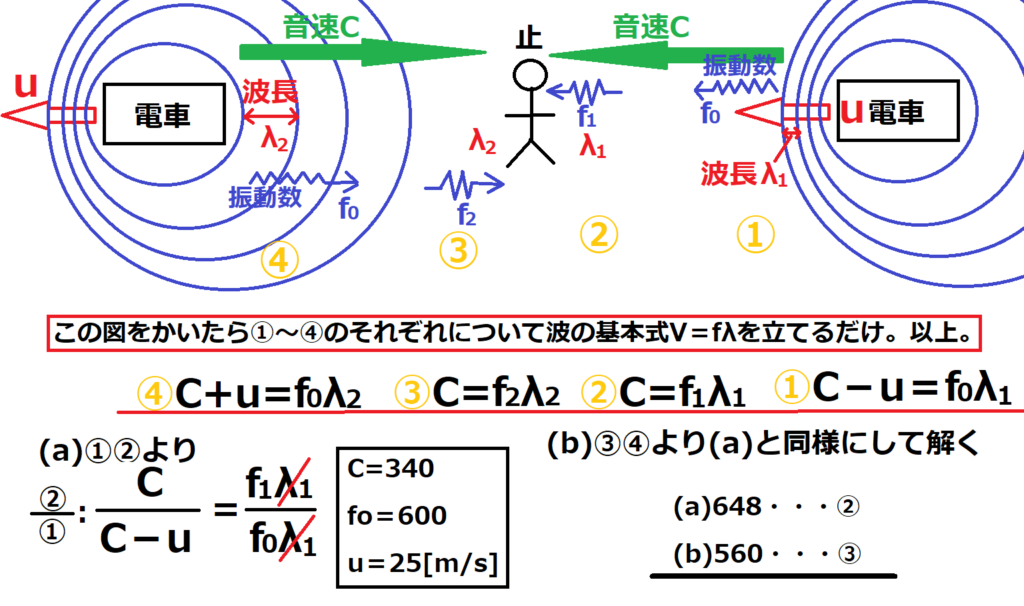
問１１【物理：ドップラー効果】答え(a)②、(b)③

航空大学校HPより引用

これ大事だから言っときます。

 

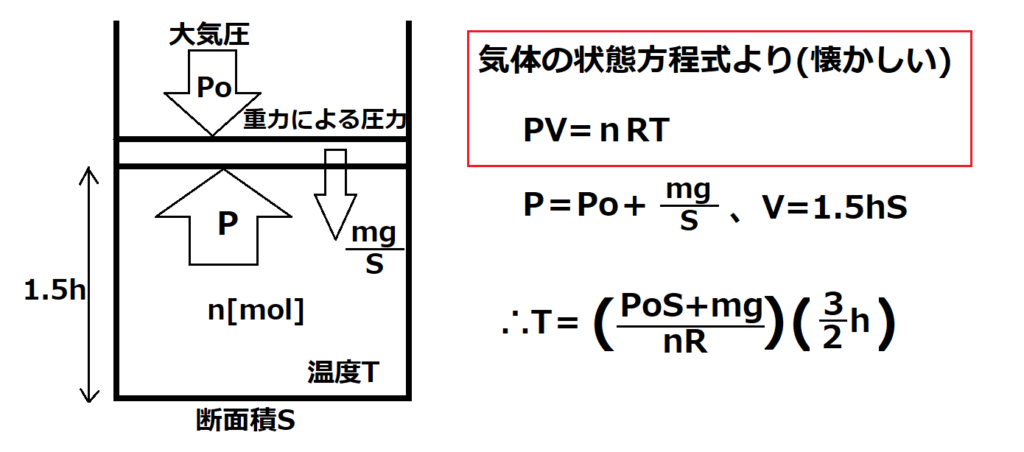
問１２【物理：熱力学】答え②

航空大学校HPより引用

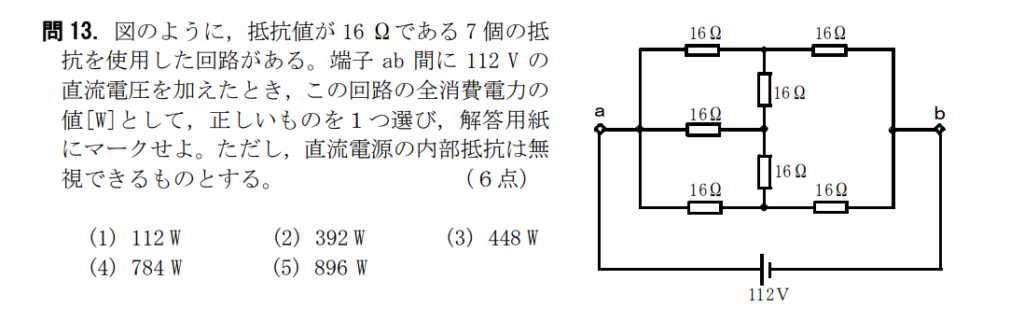
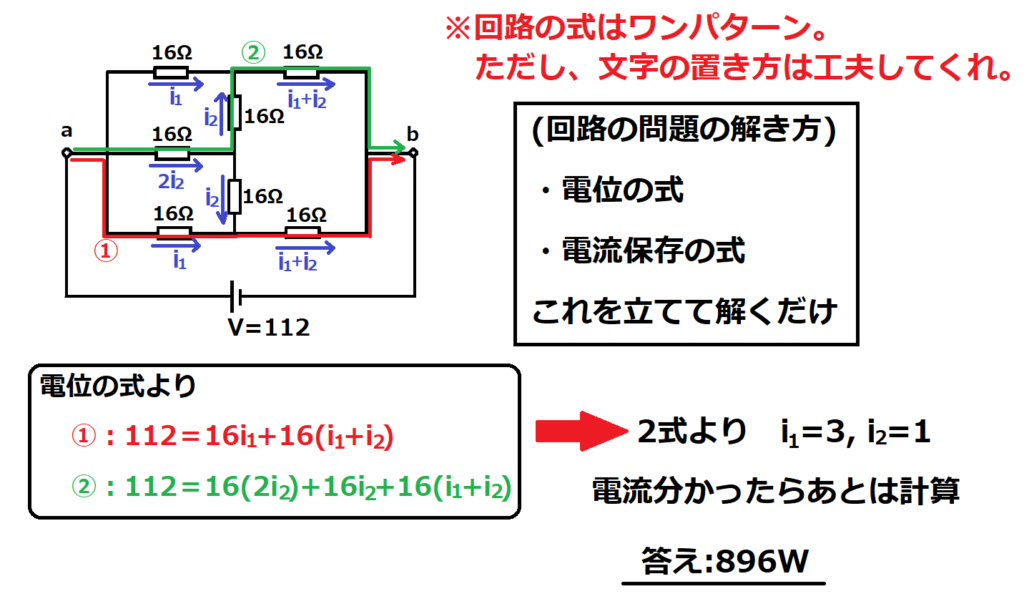
問１３【物理：電気回路】答え⑤

航空大学校HPより引用

まずi1を置いたら対称性から反対側もi1となる。i2を置くと、対称性と電流保存から真ん中は２i2となる。

こういう問題は文字の置き方が重要。

問１４【物理：電磁気】答え③

航空大学校HPより引用

一周した場合、起電力は通った磁場の面積に比例する。

全体の円の面積はπl²で、MQ間の通った面積はドーナツ状になるが３/４×πl²となる。

よって３/４倍。

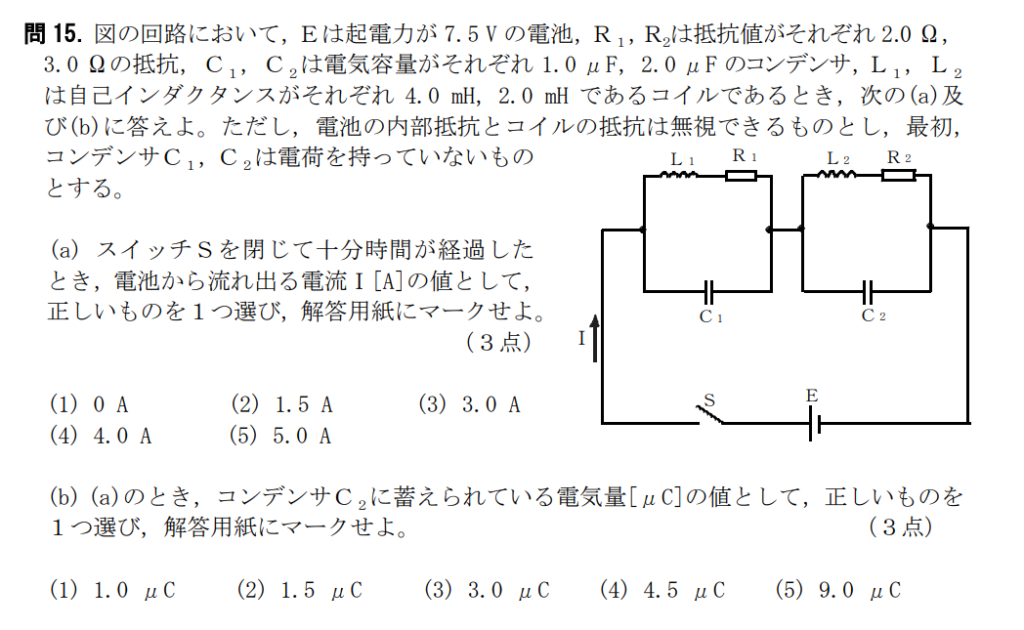
問１５【物理：電気回路】答えa②、b⑤

航空大学校HPより引用

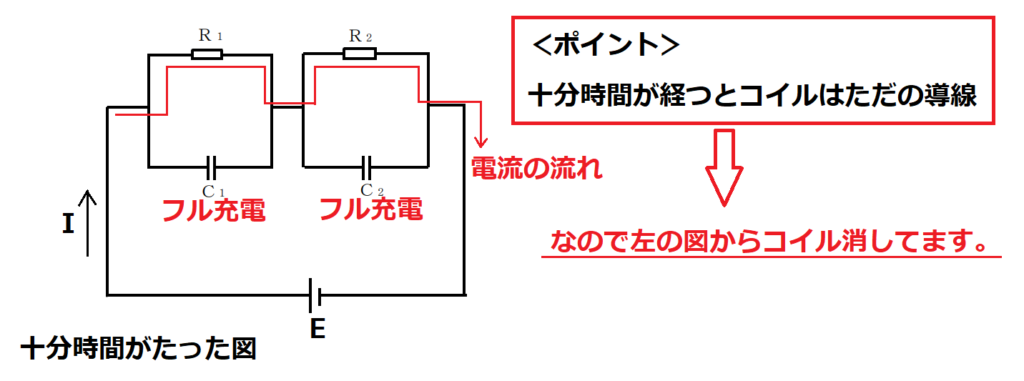
(a)

オームの法則よりE=I(R1+R2)となる。数値を入れて計算すると、I=１.５[A]

(b)

コンデンサーの基本式Q=CVを使う。コンデンサーC2の電位はR2にかかる電位と等しいので

Q2＝CV＝CIR2＝２μ×１.５×３＝９.０μ[C]

問１６【数学：ベクトル】答え④

航空大学校HPより引用

ベクトルの内積を使う。

①ｘ＋ｙ＋２ｚ－３＝０の方向ベクトルと②２ｘ－ｙ＋ｚ＋１＝０の方向ベクトルと内積の関係式で解ける。

 

①ｘ＋ｙ＋２ｚ－３＝０上の２つの点を取る。できるだけ簡単な点にする。→(０,３,０)と(３,０,０)を選択。

②２ｘ－ｙ＋ｚ＋１＝０上の２つの点を取る。→(０,１,０)と(０,０,－１)を選択。

 

問１７【数学：三角関数】答え④

航空大学校HPより引用

問１８【数学：対数】答え(a)⑤.(b)③

航空大学校HPより引用

まずは問題文の式をｘ^log2x＝x^a×６４に変形して。

６４＝２^６なのでｘ^log2x＝x^a×２^６

両辺log₂をとってlog₂ｘ^log2x＝log₂(x^a×２^６)

⇔(log₂x)²＝log₂x^a＋log₂２⁶

⇔(log₂x)²＝a×log₂x＋６・・・(１)

ここで解の１つが６４とのことなので(１)にｘ＝６４を入れる。

そうすると

(log₂６４)²＝a×log₂６４＋６

⇔６^２＝a×６＋６

⇔a＝５となる。・・・(a)の答え

a＝５を(１)に代入して

(log₂６４)²＝５log₂６４＋６

⇔(log₂x)²－５log₂x－６＝０

⇔(log₂x－６)(log₂x＋１)＝０

⇔log₂x＝６または－１

∴ｘ＝６４または１/２・・・(b)の答え

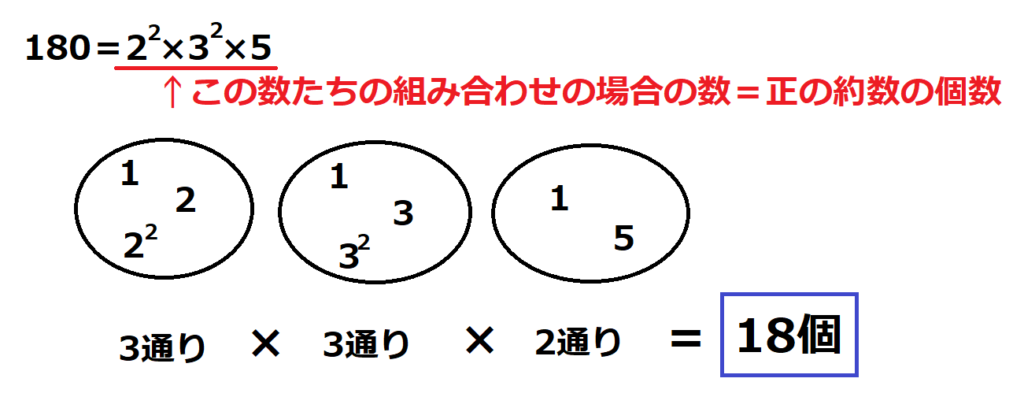
問１９【数学：正の約数の個数】答え③

航空大学校HPより引用

まずは素因数分解でその素因数がどう組み合わされるかを掛け合わせるだけ。

問２０【数学：２次関数】答え③

航空大学校HPより引用

典型的な問題。しかもｘの1次式の係数が偶数になってるのはサービス。

①の条件は

(a－３)^２－(a＋３)＞０

⇔a^２－７a＋６＞０

⇔(a－１)(a－６)＞０

⇔a＜１またはa＞６・・・(１)

 

②の条件より

f(０)＝a＋３＞０より、a＞－３・・・(２)

 

③の条件について

f(x)＝(x＋(a－３))^２＋・・・

なので軸が０より大きい条件は

－(a－３)＞０　⇔　a＜３・・・(３)

 

条件(１)～(３)より　条件を満たすaの範囲は－３＜a＜１

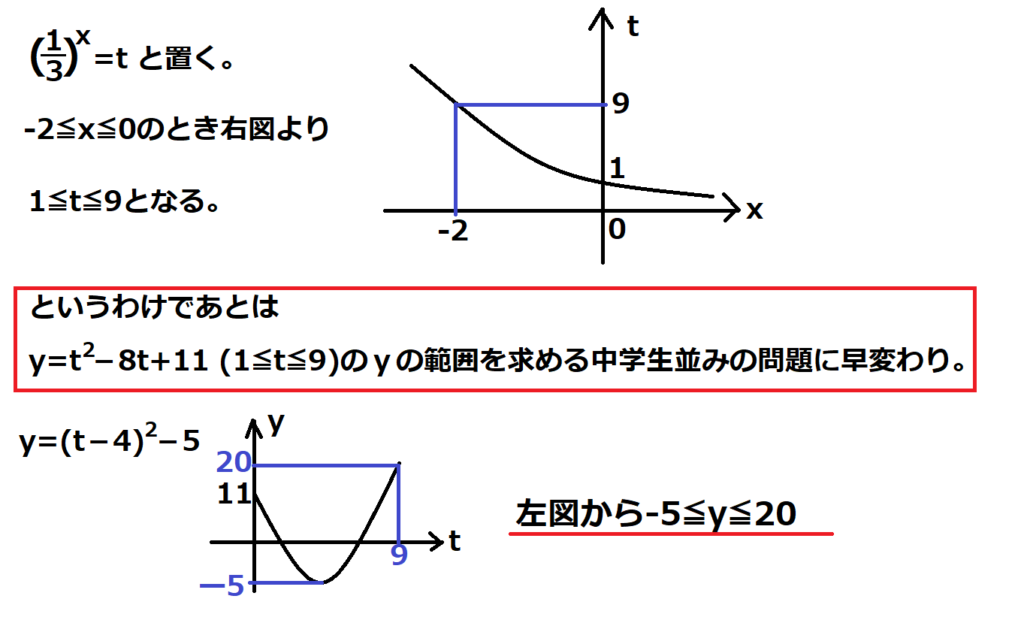
問２１【数学：指数関数】答え④

航空大学校HPより引用

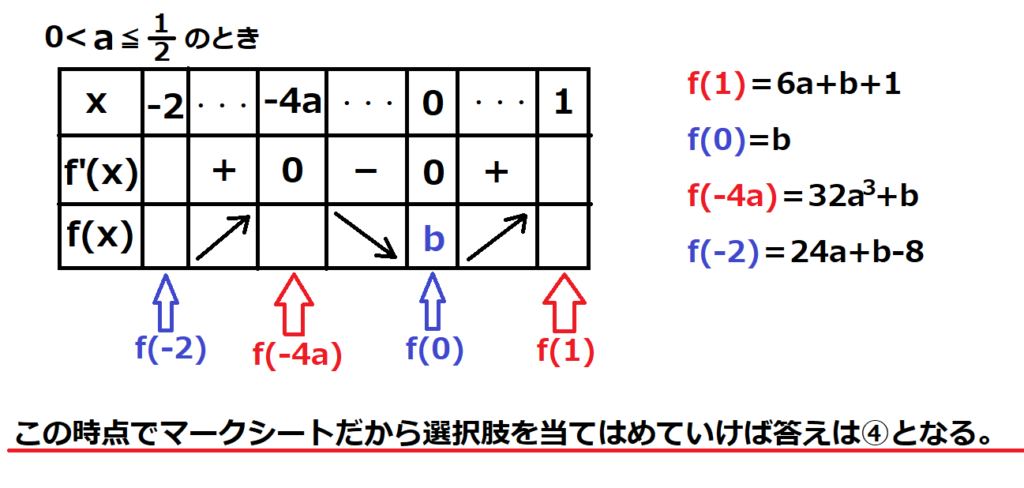
問２２【数学：微分】答え④

航空大学校HPより引用

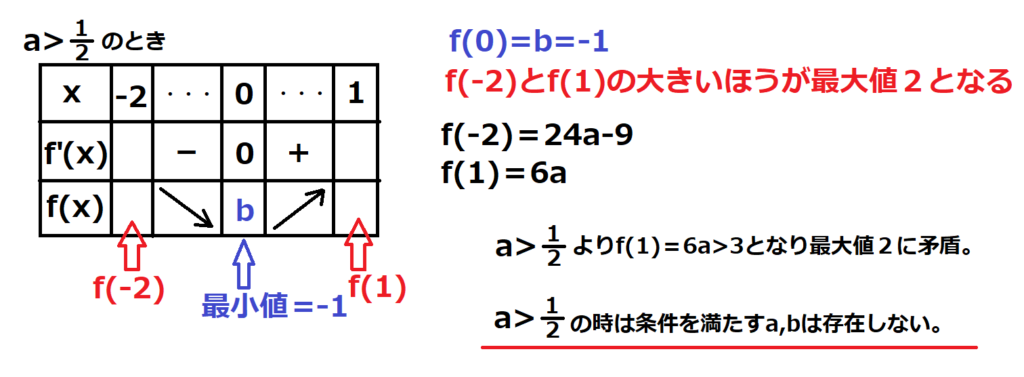
とりあえず微分する。f ‘(x)＝３x^２＋１２ax＝３x(x＋４a)なので、f ‘(x)＝０となるときｘ＝０、－４a

０＜a＜１という条件があるので、－４＜－４a＜０となる。

―２≦x≦１の範囲で考えるので、－４aが―２よりも大きい場合と小さい場合で考える必要が出てくる。

(１)－４a＜－２、つまりa＞１/２の時

(２)－２≦－４a、つまり０＜a≦１/２の時

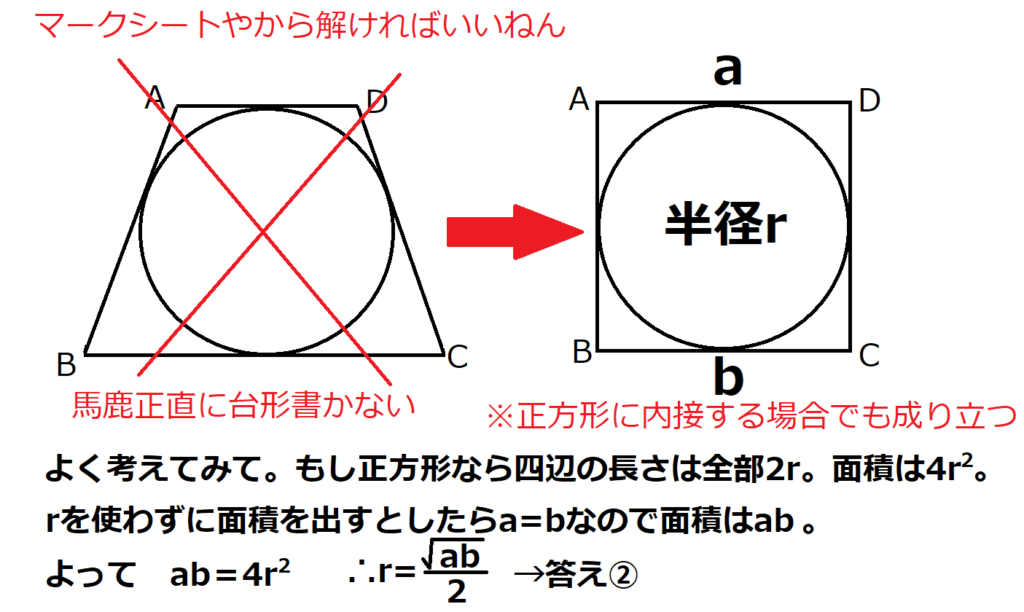
問２３【数学：等脚台形】答え②

航空大学校HPより引用

この問題はちゃんとやろうとしたら面倒やけど、これはマークシートの戦いなのでズルをします。そしたら速攻で解けます。

ちなみにこの解き方は筆記試験ならNG。

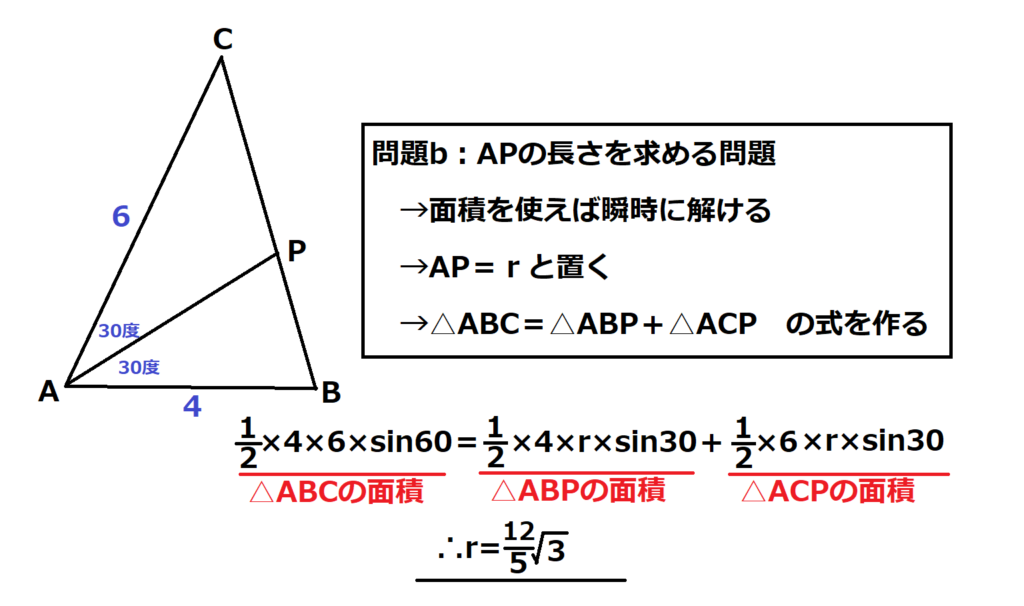
問２４【数学：図形】答え：a①.b⑤

航空大学校HPより引用

この問題のaは三角形ABCで余弦定理を使って終わり。答えは①。

問題はbのほうで余弦定理使いまくってやれば解けるけど、計算が地獄。

あるやり方をすれば瞬時に解ける。時間的に差がすごく出るのでこの解法を覚えてほしい。

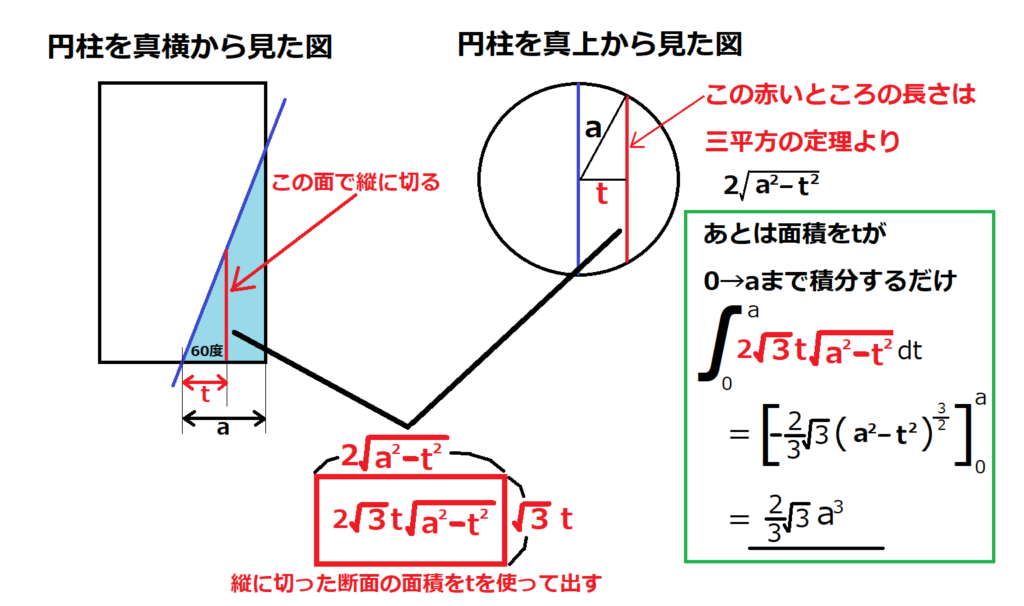
問２５【数学：積分】答え③

航空大学校HPより引用

これは積分の問題。正直言って数学が苦手な人には厳しい問題。

これができなくても合否に影響ないと思われる。

航空大学校過去問【2021年度(令和3年度)　総合Ⅱ　解答・解説】