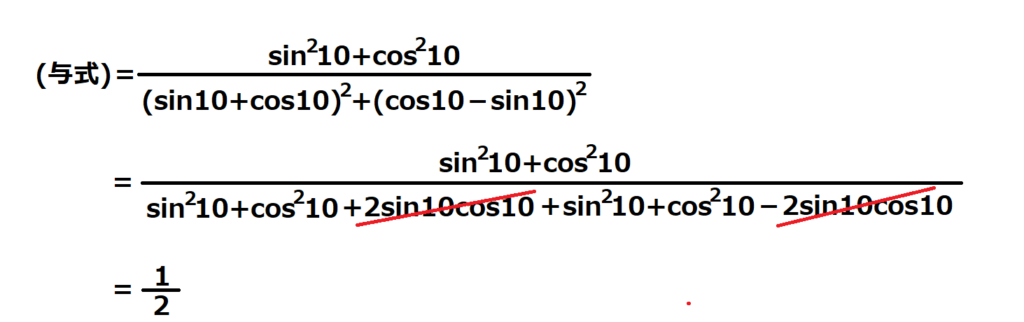航空大学校過去問解説です。
他の年度の過去問解説もありますのでブログの「航空大学校過去問解説」からチェックしてみてください。
毎年同じような問題なので傾向と対策は立てやすいかと思います。
定員が増えてからは1次試験の倍率は3倍程度です。
でも、ただ解くだけではなく、できるだけ最短の解き方をしています。
僕の解説のように解けば余った時間を他の問題に回すことができると思います。
2026年から出題範囲が変わるようなのでまず以下の記事をチェックしてみてください。
↓↓↓↓↓↓↓↓↓↓↓↓
目次
問1【時事問題:航空知識系】答え①
航空大学校HPより引用
問2【時事問題:知識系】答え⑤
航空大学校HPより引用
問3【社会:知識系】答え④
航空大学校HPより引用
問4【社会:知識系】答え①
航空大学校HPより引用
問5【地学:気象】答え④
航空大学校HPより引用
問6【化学:気象】答え③
航空大学校HPより引用
この現象のことを「フェーン現象」という。
問7【物理:等加速度直線運動】答え(a)②.(b)①
航空大学校HPより引用
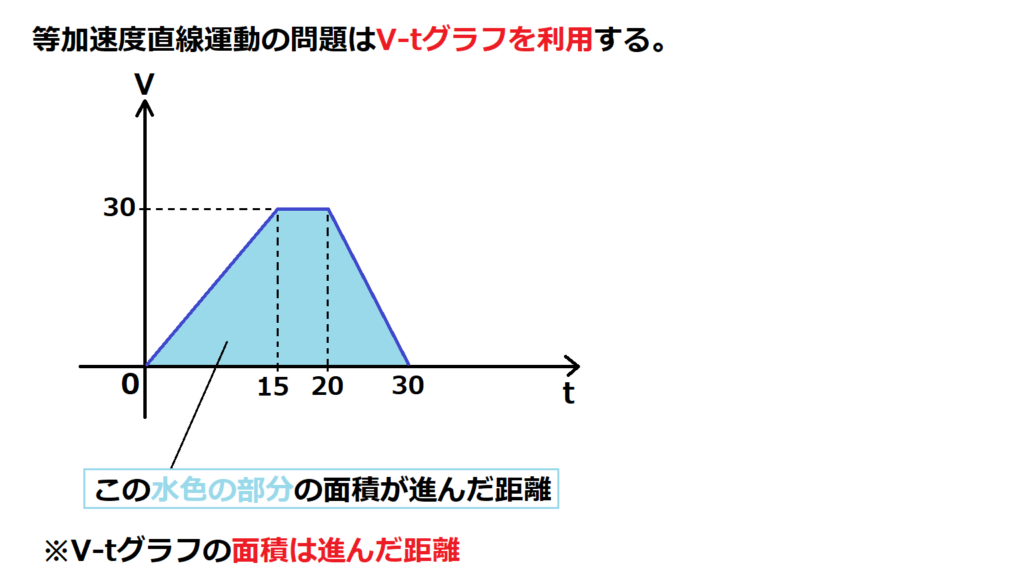
物理は単位を合わせることが大事。
速度の単位は[m/s]で計算すること。
108km/h=30m/s
停止した状態から15秒で30m/sに達したということは加速度は2m/s2。
よって面積を求めると525なので進んだ距離は525m。
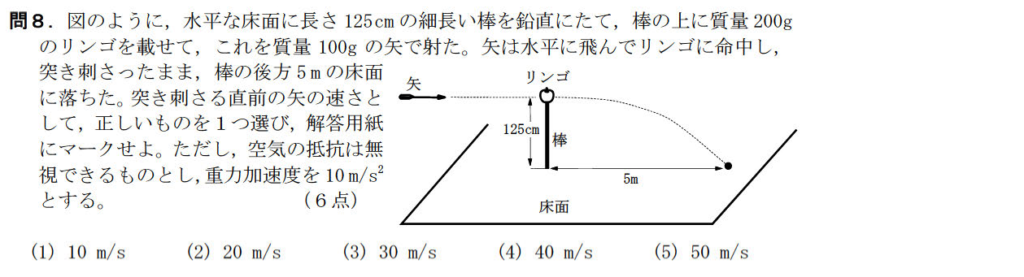
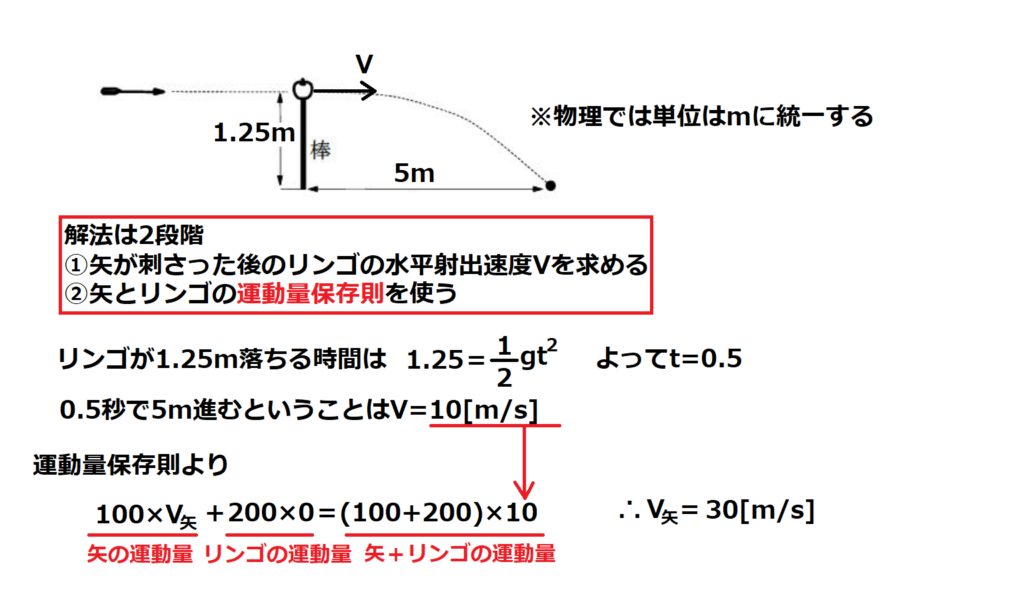
問8【物理:運動量保存則、等加速度運動】答え③
航空大学校HPより引用
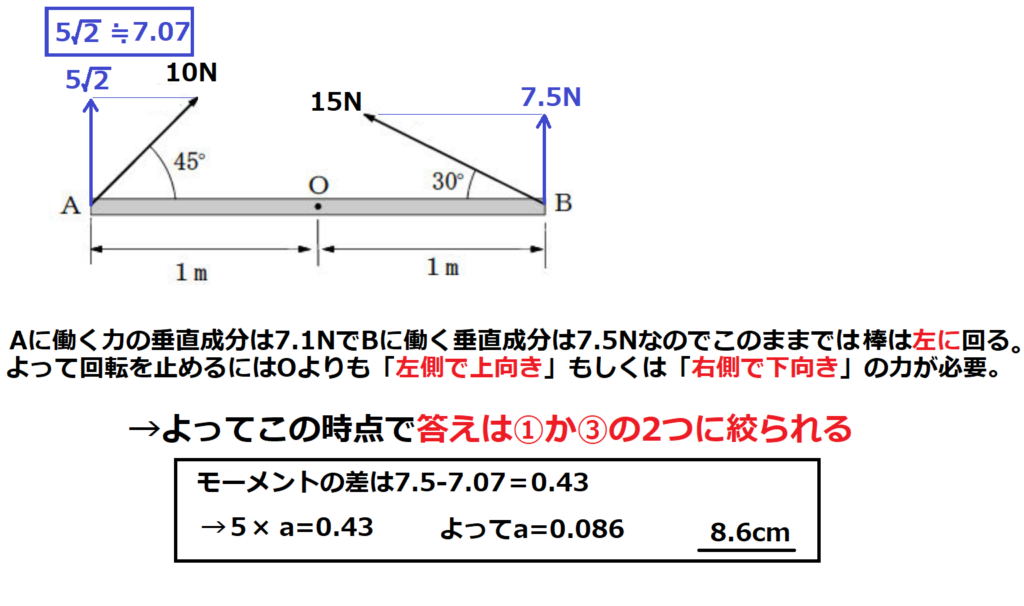
問9【物理:力のモーメント】答え①
航空大学校HPより引用
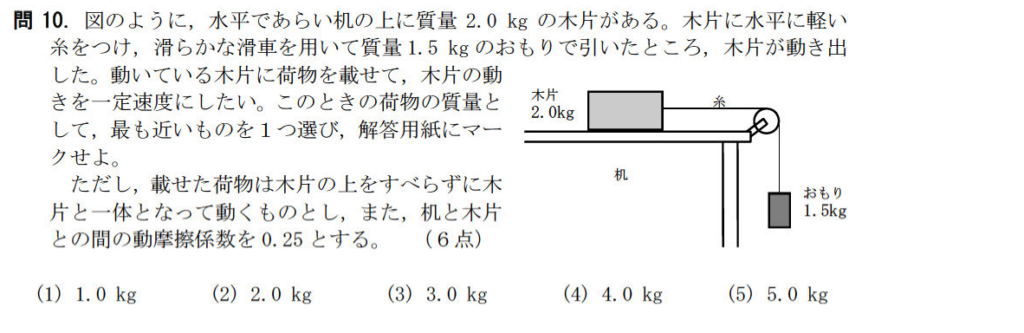
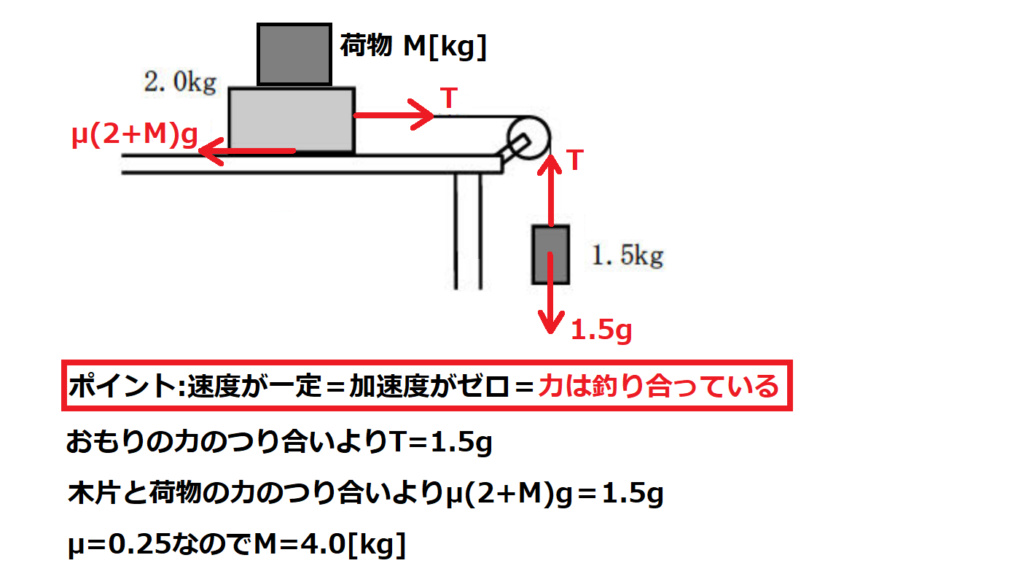
問10【物理:力学】答え④
航空大学校HPより引用
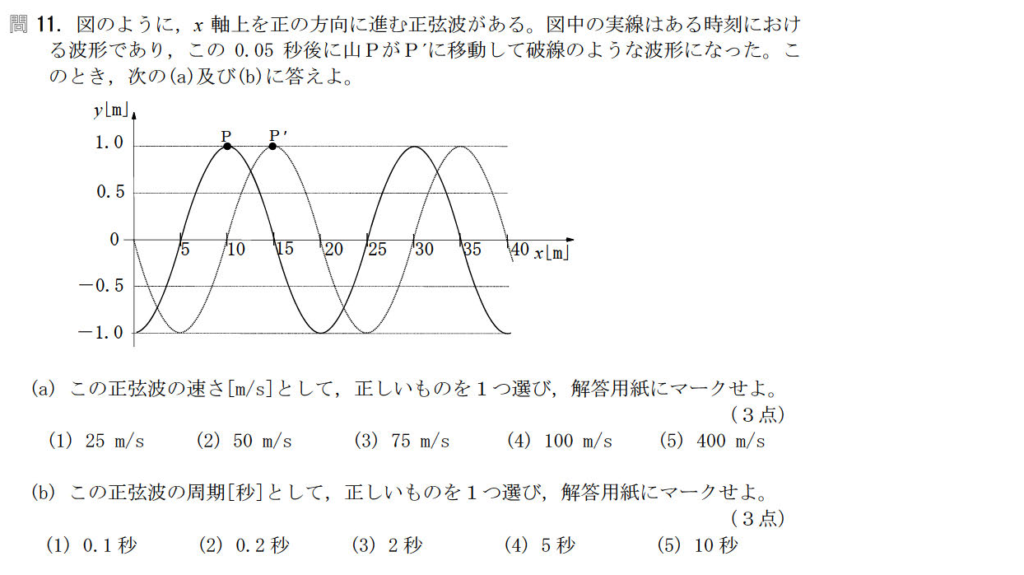
問11【物理:波動】答え(a)④.(b)②
航空大学校HPより引用
この波は正の方向(右向き)に進んでいる。たまに左に進むというひっかけもあるので問題文はよく読むこと。
波動の問題は苦手な人が多い。
その理由は公式だけを丸暗記しているから。
振動数の単位[Hz(ヘルツ)]の意味を押さえること。
(a)については5m進むのに0.05秒なので速さは100m/sとなる。
(b)波動の基本式V=fλより、f=5[Hz]
T=1/f=0.2
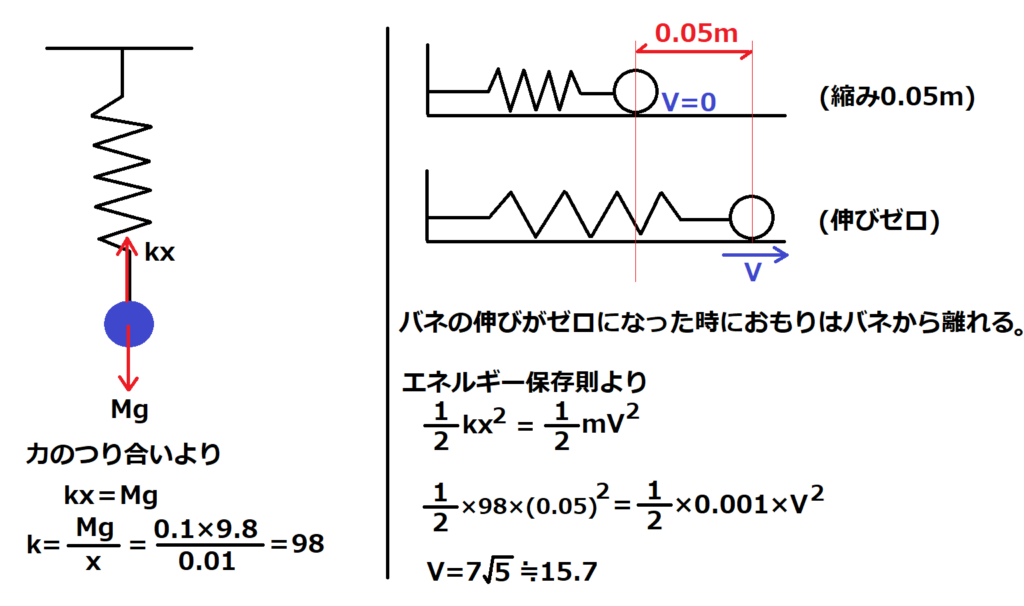
問12【物理:バネ】答え②
航空大学校HPより引用
簡単な問題だけど単位だけしっかりすること。
物理の単位はメートル、キログラム。
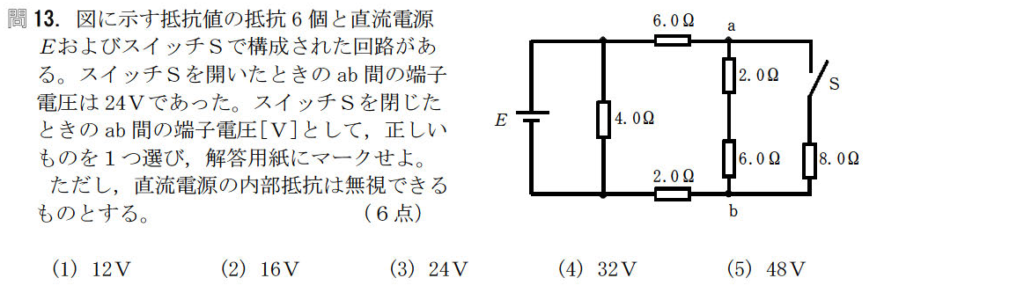
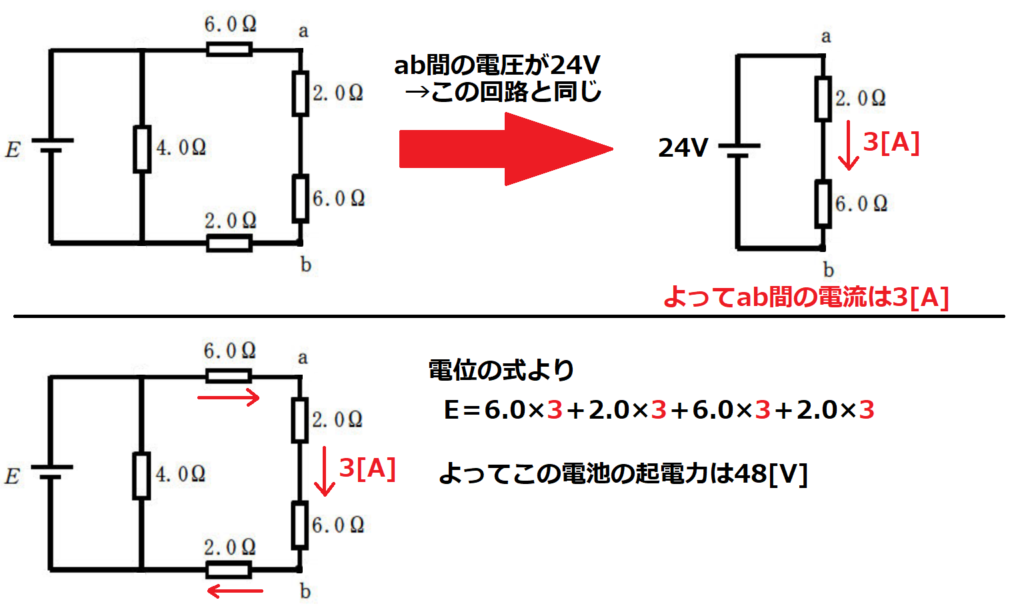
問13【物理:電気回路】答え②
航空大学校HPより引用
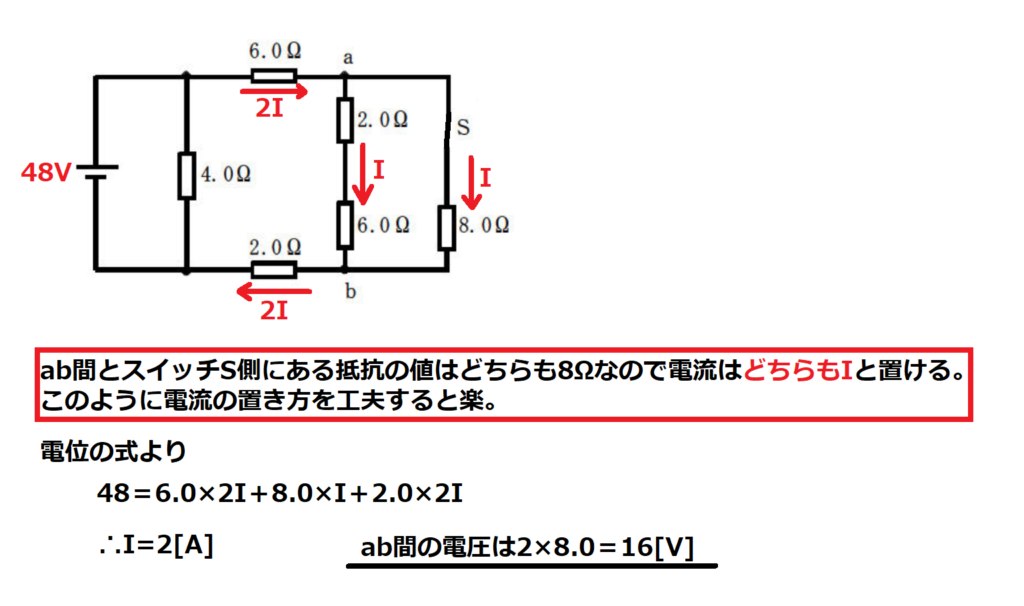
次にスイッチSを閉じた時の回路を考える。
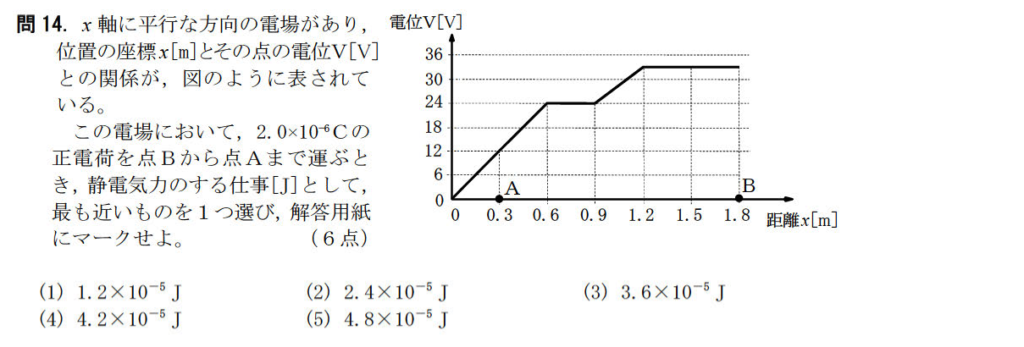
問14【物理:力学】答え④
航空大学校HPより引用
この問題は電位とは何かが分かっている人にとっては優しい問題。
A点での電位は12VでB点での電位は33Vなのでその差は21Vとなる。
よって2.0×10-6Cの正の電荷がする静電気力の仕事は2.0×10-6×(33-12)=4.2×10-5[J]
※電圧とは1[C]の位置エネルギー
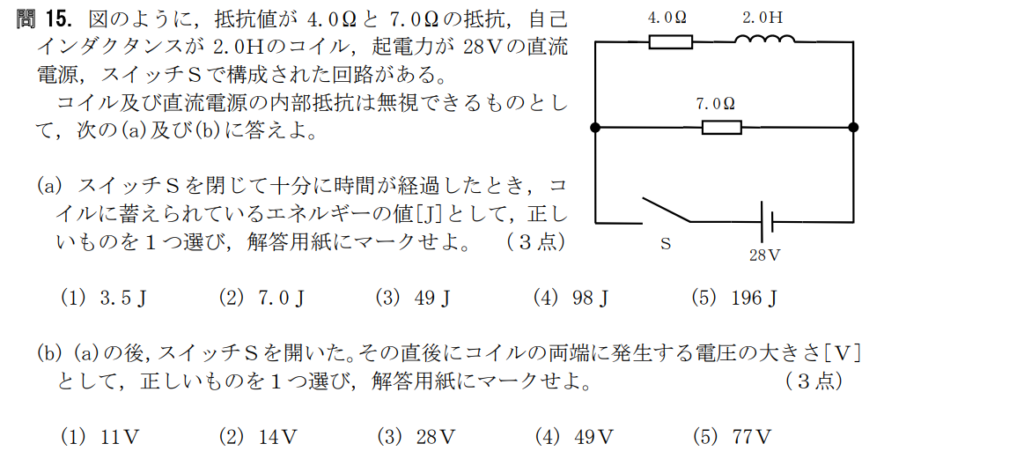
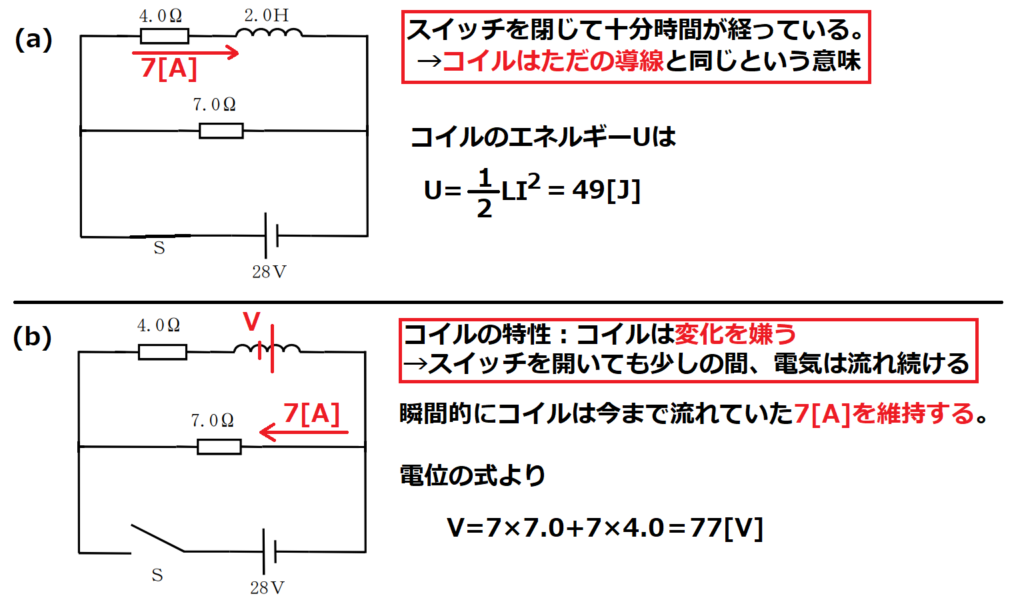
問15【物理:電気回路】答え(a)③.(b)⑤
航空大学校HPより引用
コイルの問題が出たらラッキー。
微分積分を使った物理は出題されないので、コイルの問題はコイルに電流が流れて十分時間が経った場合か、電流を流したり切ったりした直後の場合しか出題されない。
問16【数学:2次方程式】答え②
航空大学校HPより引用
因数分解すると、(x+1){x+(k-1)}=0
解は-1、1-kの2つ。
1-k=-2のとき、k=3
1-k=-1/2のとき、k=3/2
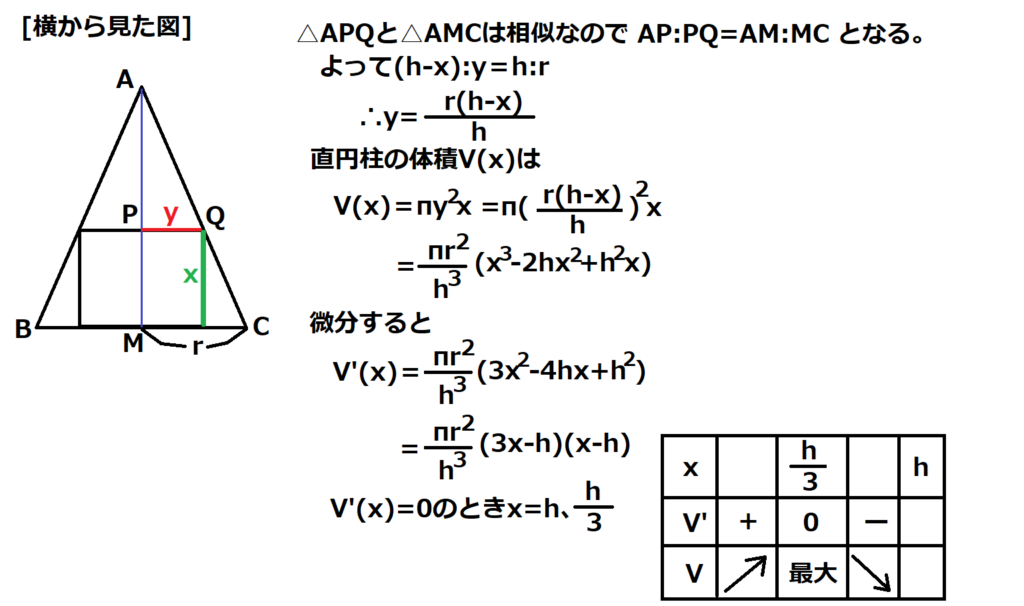
問17【数学:微分】答え②
航空大学校HPより引用
問18【数学:数式問題】答え(a)②.(b)④
航空大学校HPより引用
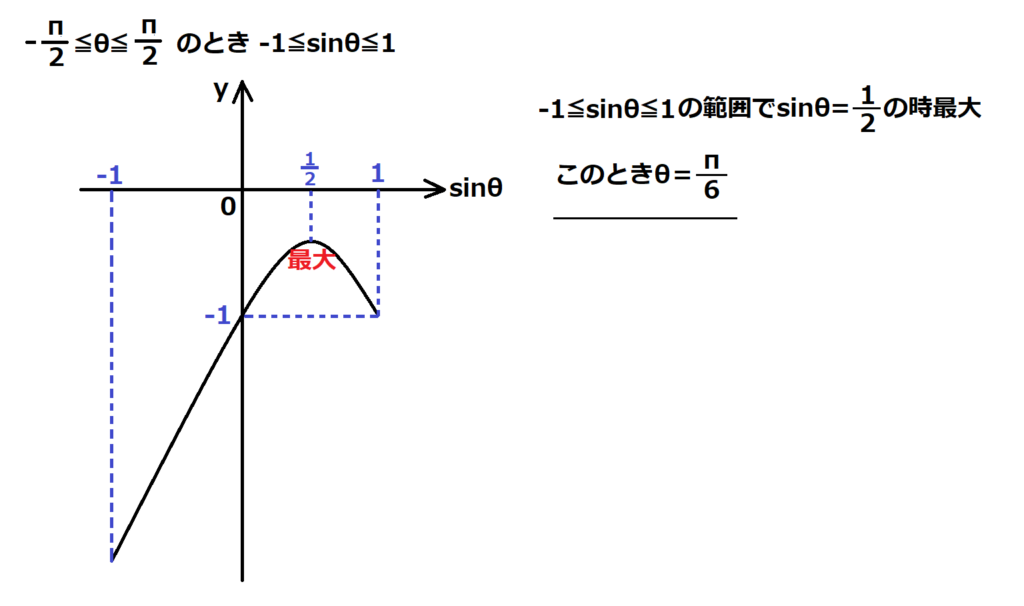
問19【数学:2次関数】答え②
航空大学校HPより引用
sinθとcosθが混ざっていると計算できないので「sin2θ+cos2θ=1」を使ってsinθに統一する。
関数は
y=2sinθ+2(1-sin2θ)-1
=-2sin2θ+2sinθ-1
=-2(sinθ-1/2)2-1/2
と変形できる。
問20【数学:三角関数】答え③
航空大学校HPより引用
よって後は計算するだけ。
sin80とcos80を全てcos10とsin10に置き換えてsin10とcos10だけの式にする。
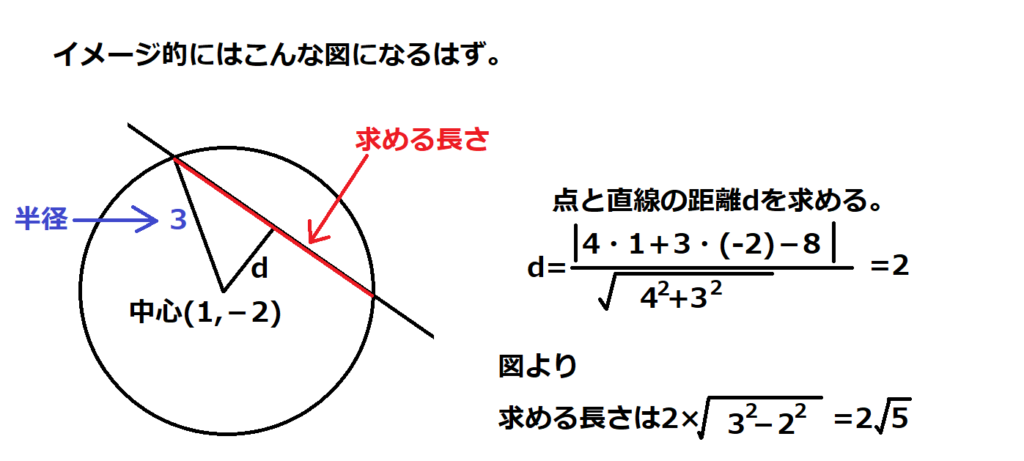
問21【数学:図形】答え①
航空大学校HPより引用
この問題は2式を連立してxかyどちらかを消去して2次方程式を解いて直線と円の交点の座標を出せば解ける。
が、計算が地獄なのでやめておく。図形的に考える。
この円の方程式は(x-1)2+(y+2)2=9と変形できることから中心が(1,-2)で半径3の円である。
問22【数学:2次方程式】答え④
航空大学校HPより引用
ルートは2分の1乗と同じ意味。
方程式の両辺に7xをかける。
そうすると、方程式は7x-2・7x/2-3=0となる。
因数分解すると(7x/2-3)(7x/2+1)=0より
7x/2=3 (-1の方は負の数なので不適切)
両辺log7をとる。
x/2=log73
∴x=2log73
問23【数学:対数関数】答え③
航空大学校HPより引用
選択問題なので最悪分からなければひとつずつ代入していけば答えは出る。(ここではやらない)
対数関数の計算では底をそろえるのが重要。
言うまでもなくこの問題では底を3にそろえる。
logx3=1/log3x (底と真数を入れ替えると逆数になる)
底を3でそろえたら両辺に(log3x)2をかける。
2(log3x)3+3(log3x)2-1=0
因数分解すると
{(log3x)+1}2(2log3x-1)=0
log3x=-1、1/2
∴x=1/3、31/2(←ルート3)
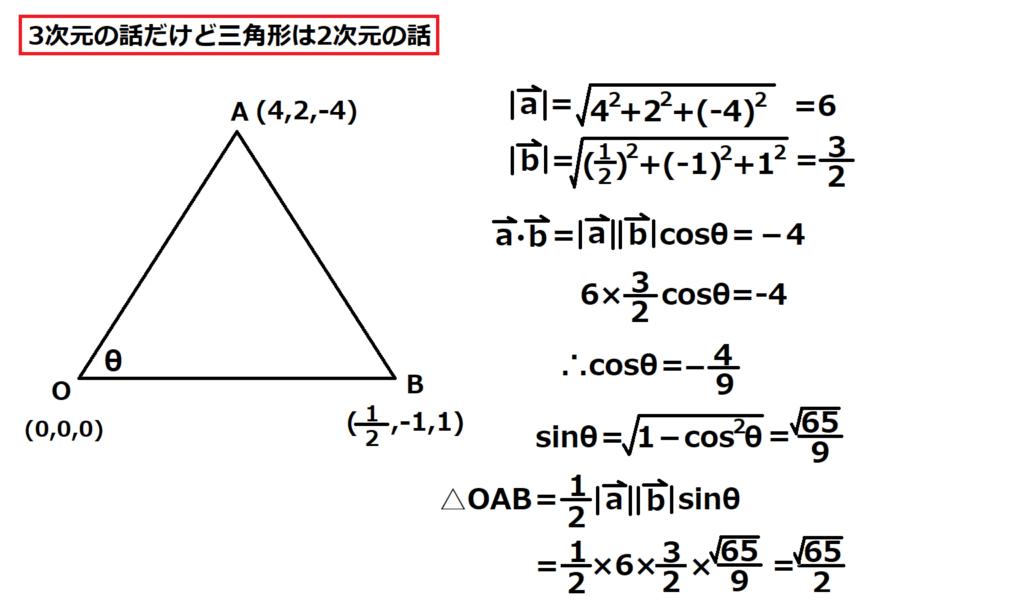
問24【数学:ベクトル】答え(a)①.(b)④
航空大学校HPより引用
(a)内積の計算問題。
(a,b,c)と(x,y,z)の内積はax+by+czになるのでベクトルaとベクトルbの内積は-4
問25【数学:積分】答え⑤
航空大学校HPより引用
絶対値を含んだ定積分はしっかり図を書く。
図の書き方を順を追って説明するので覚えてください。
全部で3Step。
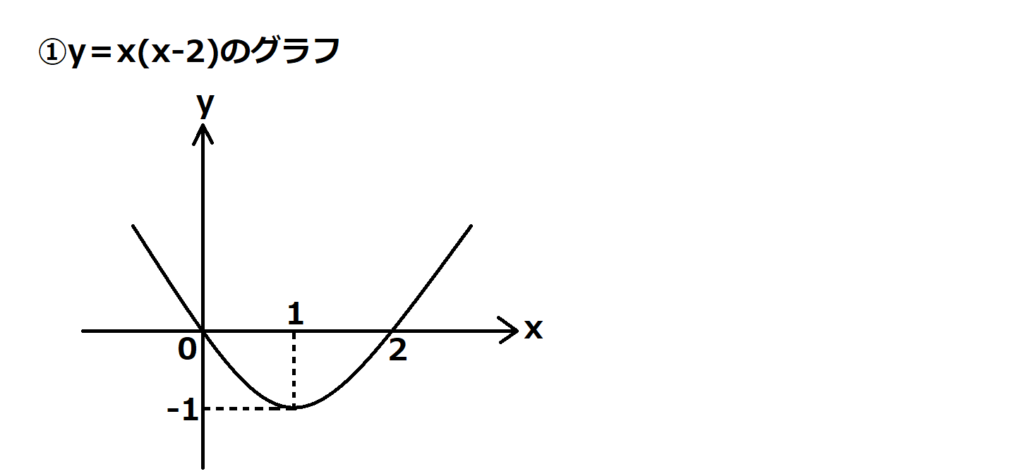
①まず絶対値の中のグラフを書く
つまりy=x2-2x=x(x-2)のグラフを書く。
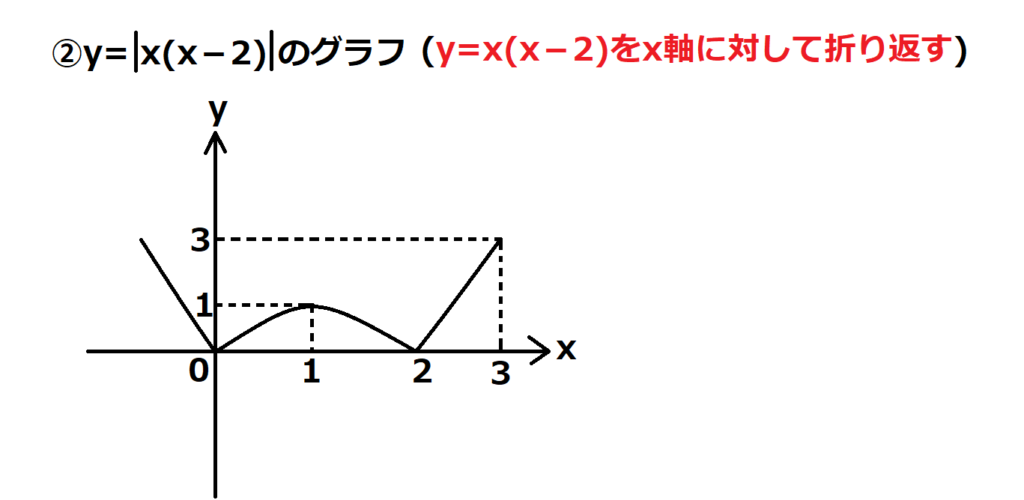
②次に絶対値を含んだグラフを書く。
つまりy=|x(x-2)|のグラフを書く。
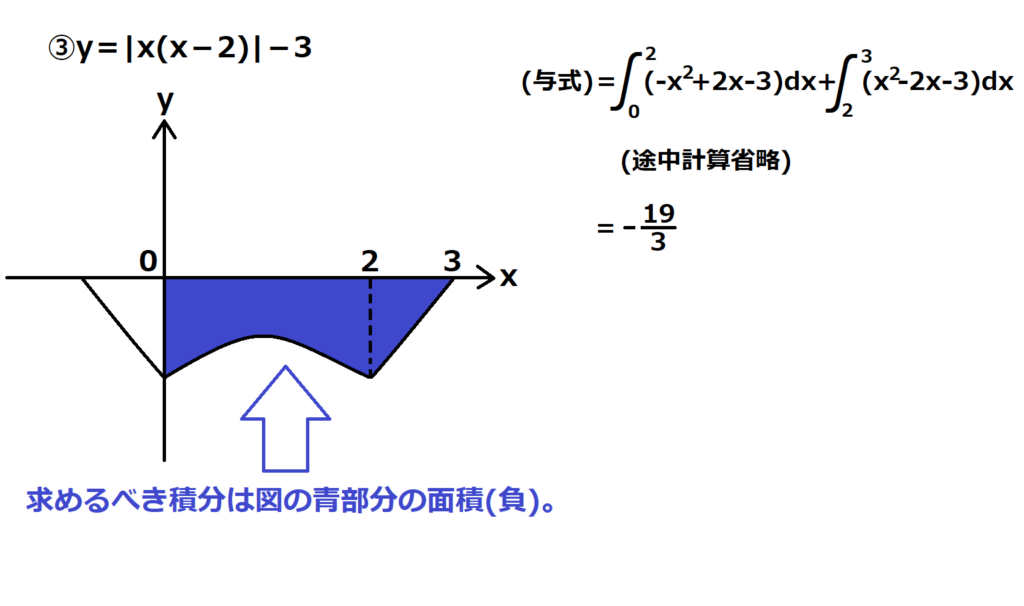
③最後にy=|x(x-2)|-3のグラフを書く。
②のグラフをy軸方向に-3動かせばよい。
→この「絶対値を含んだ定積の計算問題」は2015年度の問25でも出題されている。
やり方を覚えてしまいましょう。これからも出る可能性が十分あります。