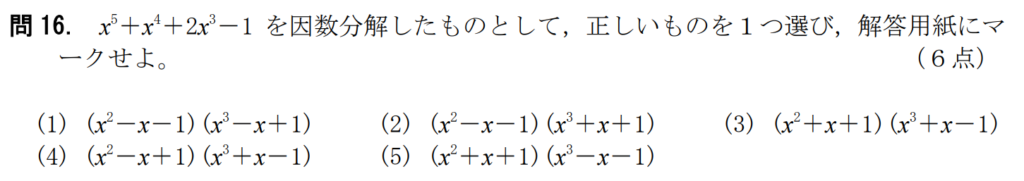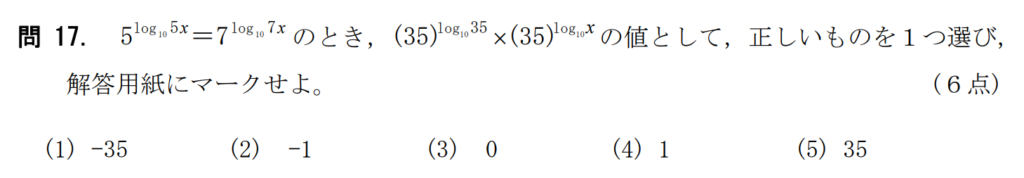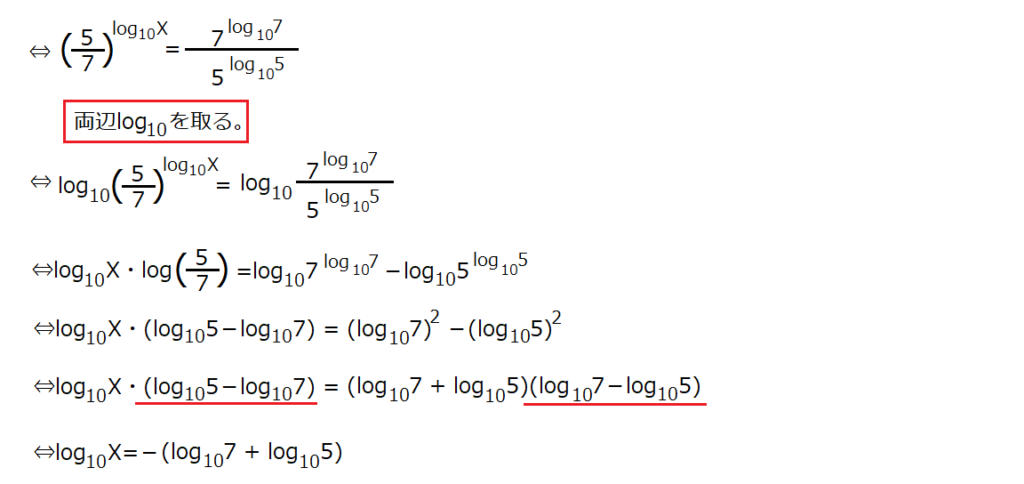航空大学校過去問解説です。
毎年同じような問題なので傾向と対策は立てやすいかと思います。
この年度は計算問題が少なく、概念・定義自体を問う問題が多かったので60分を切ることが可能です。
ただ、「ダイオード」「LC回路の電気振動」や「法線」などのやや珍しいマニアックな問題が出題されている。
ただ解くだけではなく、できるだけ最短の解き方をしています。
僕の解説のように解けば余った時間を他の問題に回すことができると思います。
2026年から出題範囲が変わるようなのでまず以下の記事をチェックしてみてください。
↓↓↓↓↓↓↓↓↓↓↓↓
目次
問1【航空系時事問題】答え④
航空大学校HPより引用
問2【時事問題】答え⑤
航空大学校HPより引用
その年にしかないイベントや、歴史的出来事は出題されやすい。
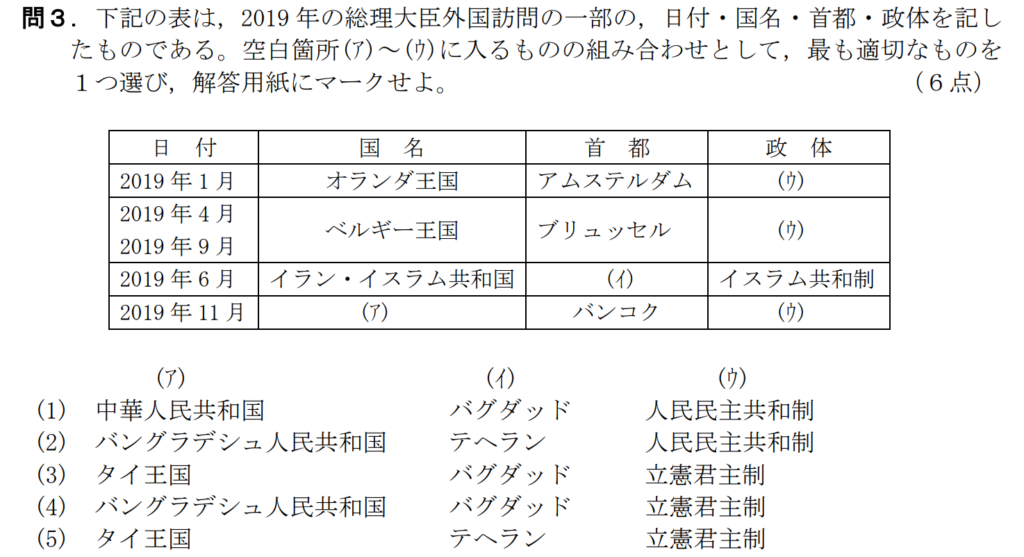
問3【一般教養】答え⑤
航空大学校HPより引用
(ア)(イ)が分かれば(ウ)は知らなくても正解できる。
個人的感想だが、タイの首都が「バンコク」は常識。
バグダッドはイラクの首都であるため、消去法で⑤が正解。
問4【時事問題:法律】答え⑤
航空大学校HPより引用
(イ)国民年金は20歳からを維持
(ウ)公営競技も20歳の基準を維持
(エ)男女ともに婚姻開始年齢は18歳となった
問5【地学:地球温暖化】答え③
航空大学校HPより引用
問6【化学:水の状態変化】答え①
航空大学校HPより引用
問7【物理:波動】答え(a)③.(b)④
航空大学校HPより引用
(a)波長は図より600mm。
(b)波の基本式V=fλより、300=f×0.6
∴f=500[Hz]
問8【物理:運動量と力積の関係】答え④
航空大学校HPより引用
運動量と力積の定義の問題。
知っているか知っていないかの問題。
(運動量の変化=加えた力積)
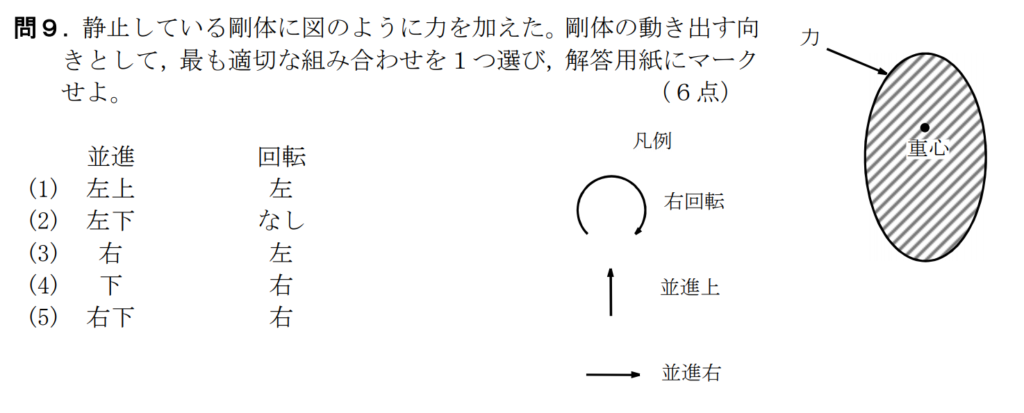
問9【物理:力のモーメント】答え⑤
航空大学校HPより引用
この問題も全問と同じで計算式のいらない問題。
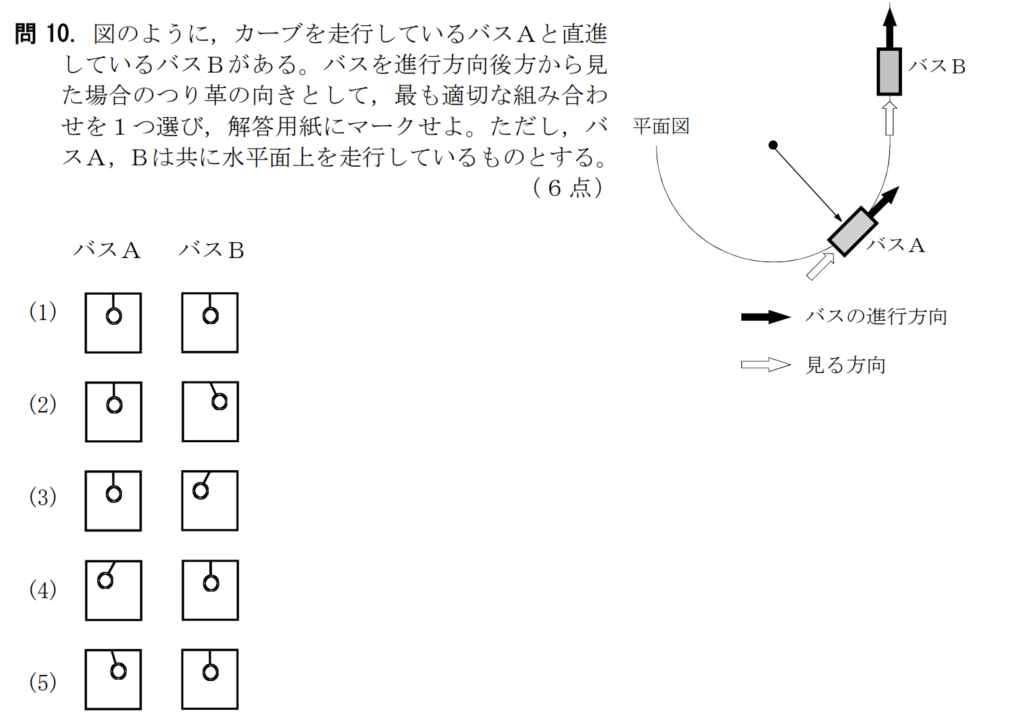
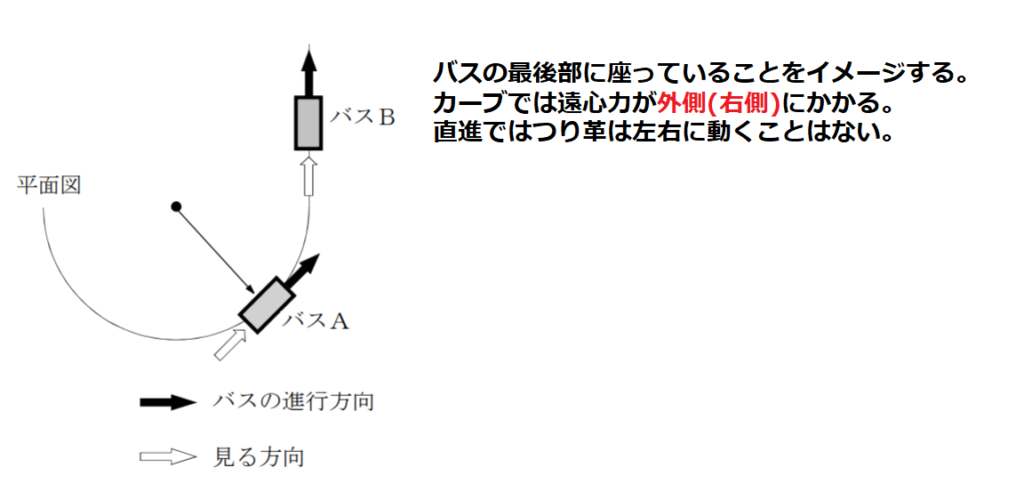
問10【物理:運動方程式】答え⑤
航空大学校HPより引用
この問題も計算式はいらない問題。
問われていることを勘違いしないように問題文をしっかり読むこと。
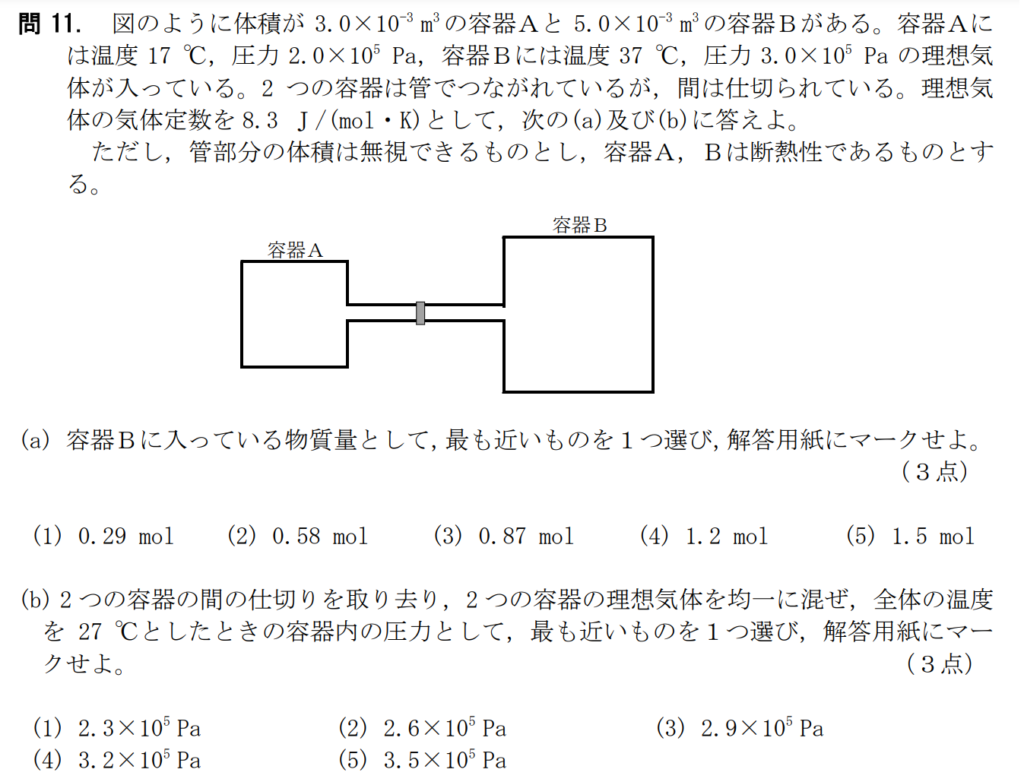
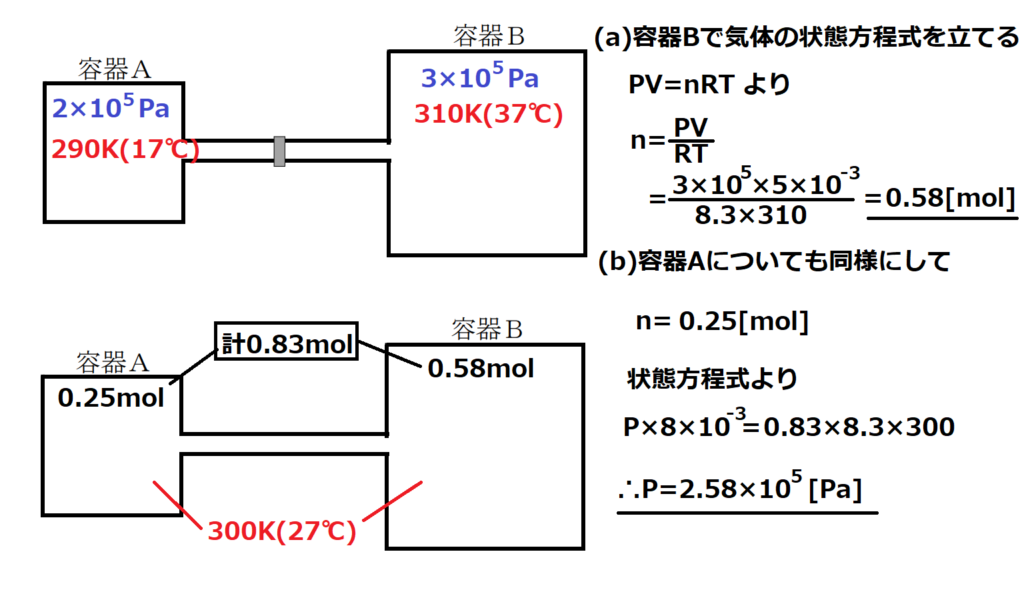
問11【物理:熱力学】答え(a)②.(b)②
航空大学校HPより引用
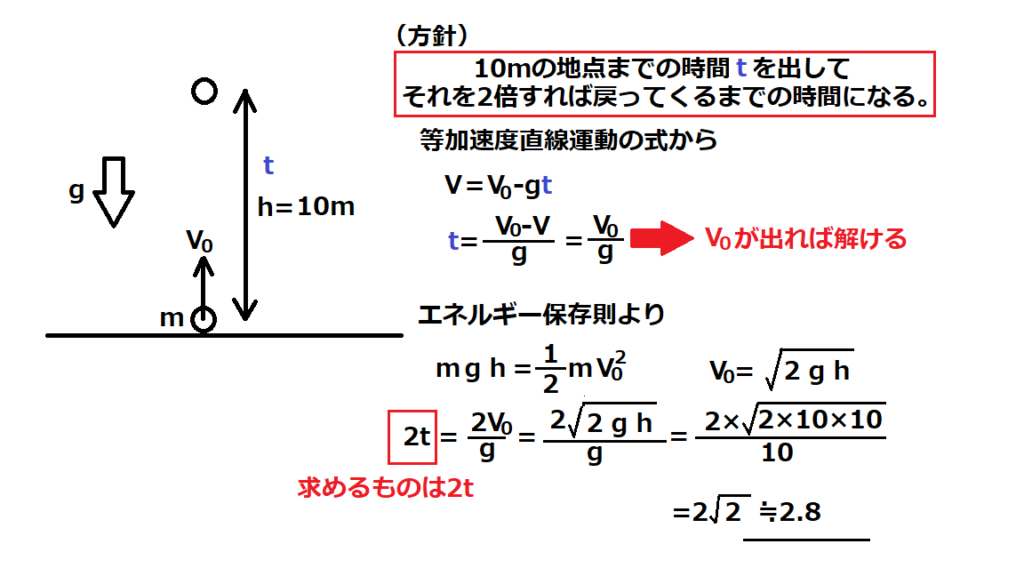
問12【物理:等加速度直線運動】答え③
航空大学校HPより引用
物理が苦手な人は、力学はどんな簡単な問題でも図を描くことをお勧めする。
現象を正確につかむことが重要。
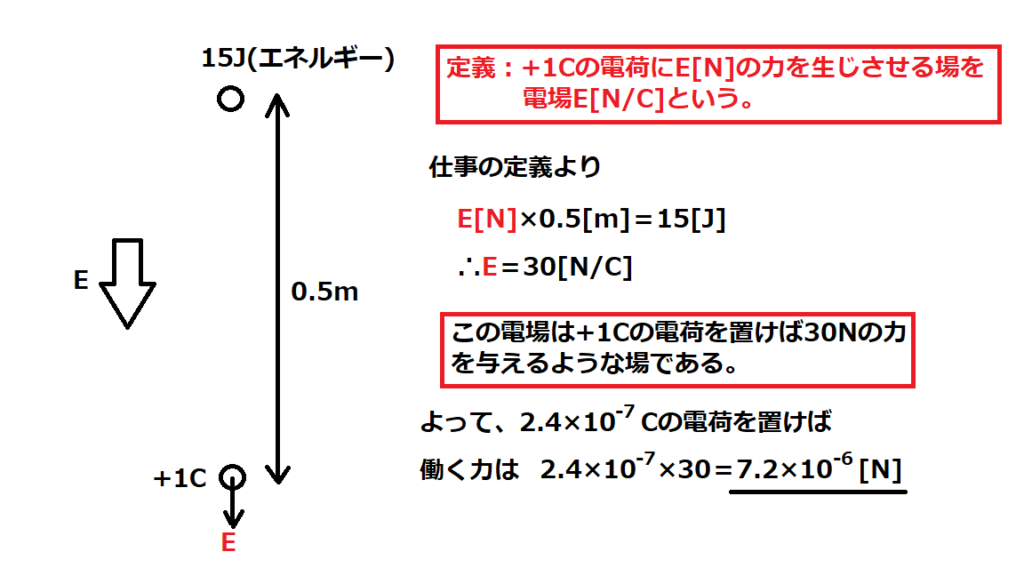
問13【物理:電磁気】答え③
航空大学校HPより引用
電場、電位の定義を知っていたら余裕の問題。
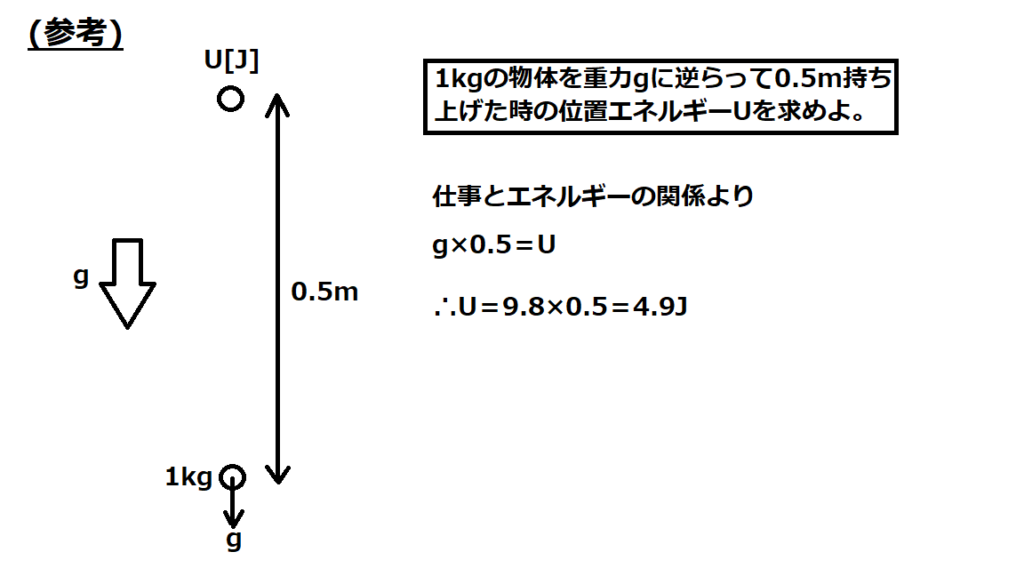
【定義】電位は、電場に逆らって+1[C]の電荷を動かしたときの位置エネルギー
電場(電界)と同じ場の力としては重力がある。それと同等に考えるとわかりやすい。
このグラフの意味は、「一様な電場E(+1Cの電荷を置いたら電荷がE[N]の力を受ける場)に逆らって0.5m移動させたら15[J]のエネルギーを得た」という意味。
この問題は、力の大きさ、すなわち電場の大きさを聞いている。
+1Cを置いたときにEの力を受ける電場をEとすると、求める答えはE×2.4×10-7である。
電場の大きさを求めれば終了だが、それはそのままグラフに書いてある。
一様な電場E(+1Cの電荷を置いたら電荷がE[N]の力を受ける場)に逆らって0.5m移動させたら15[J]のエネルギーを得たということを式にすると以下のようになる。
見てもらったらわかるように完全に力学の問題。下の問題と構造は同じ。
つまり、定義さえ押さえれば全く怖くない。
できる人は10秒くらいで解ける問題。やっていることは30×2.4×10-7の計算をしているだけ。
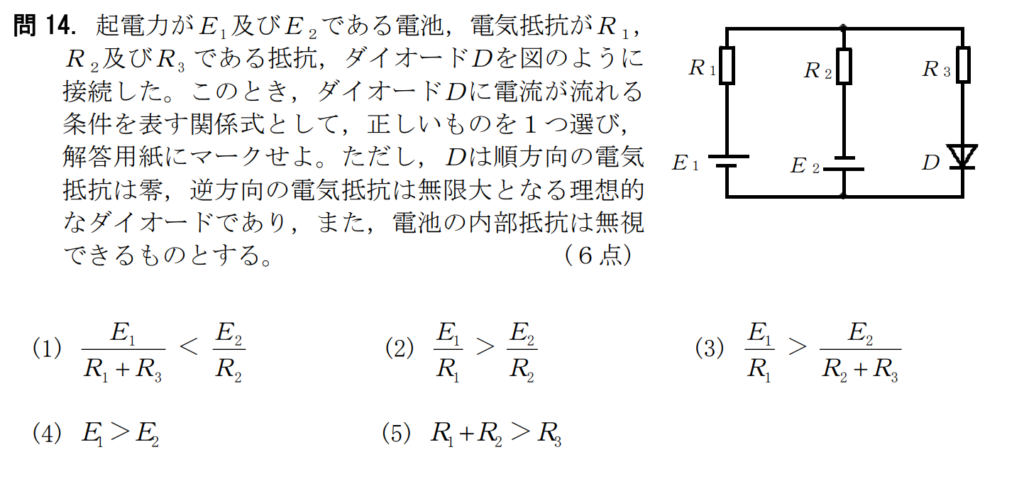
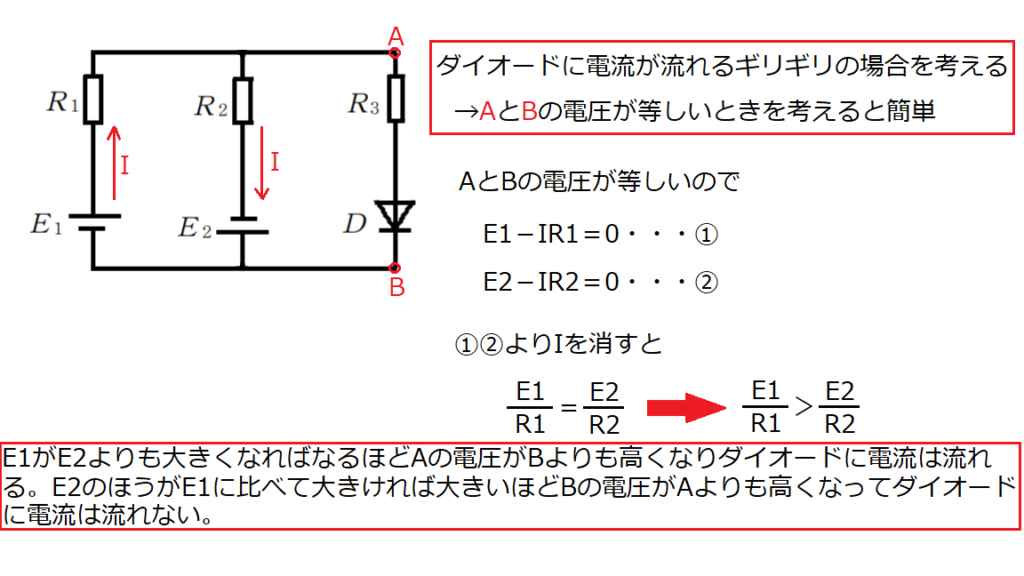
問14【物理:電子回路】答え②
航空大学校HPより引用
ダイオードとは電流を一方通行にしか流さない機器である。
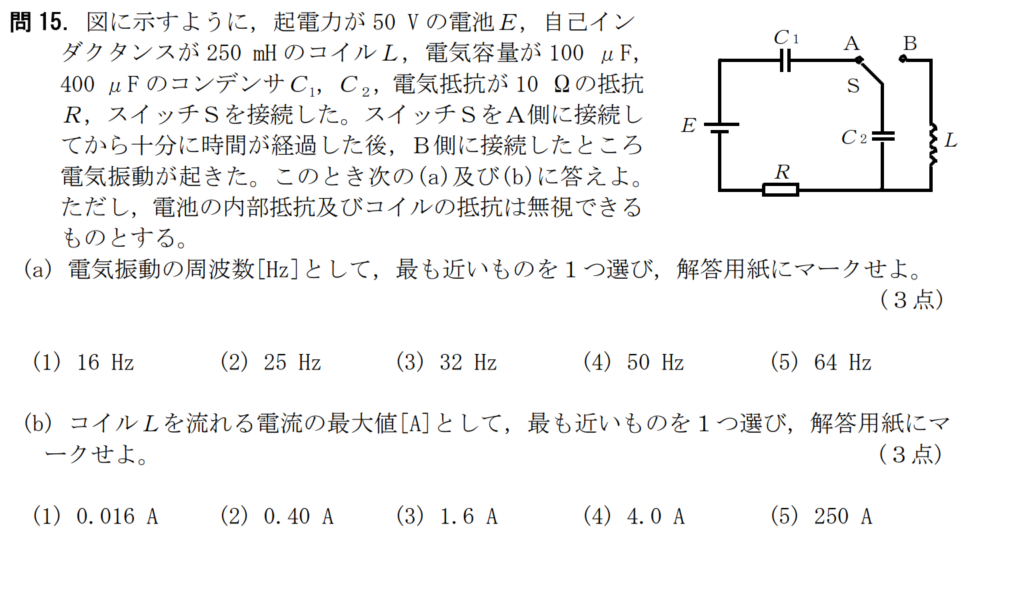
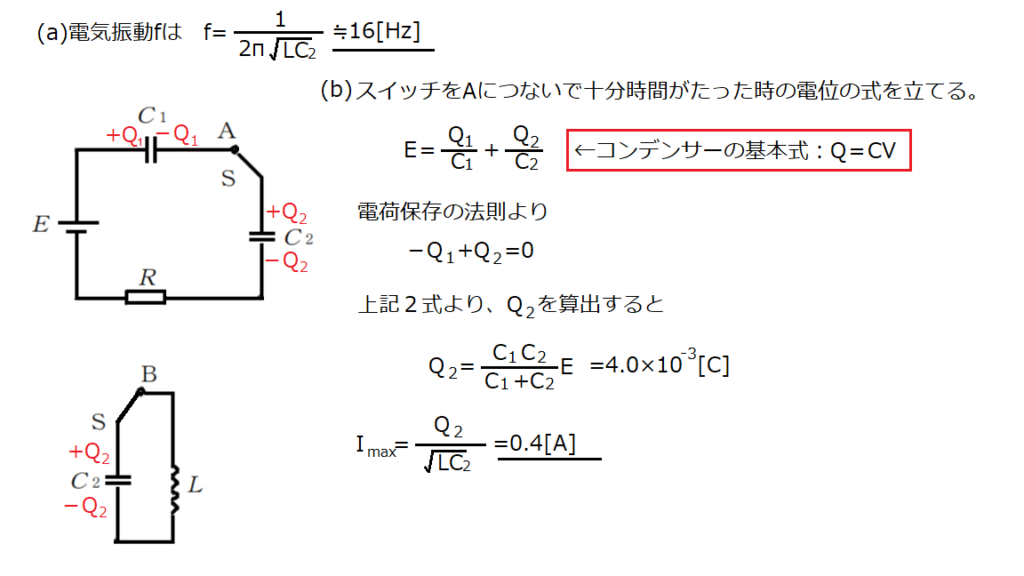
問15【物理:電子回路】答え(a)①.(b)②
航空大学校HPより引用
コンデンサーの問題で重要な一文「十分に時間が経過した後」という文言を見逃さないこと。
十分に時間が経過した後はコンデンサーは充電され、回路に電流は流れない。
よって抵抗に電流は流れない。まずは現象を正確に捉えること。
問16【数学:因数分解】答え③
航空大学校HPより引用
毎回言っているが、因数分解の選択問題は最悪選択肢を展開していけば解ける。
x5+x4+2x3-1=x5+x4+x3+x3-1
=x3(x2+x+1)+(x-1)(x2+x+1)
=(x2+x+1)(x3+x-1)
問17【数学:対数関数】答え④
航空大学校HPより引用
方針として(35)log1035×(35)log10Xの値を求めるにあたって、log10Xの値がわからないのでとりあえずlog10Xを求める。
方針:条件式を変形していってlog10Xを求める。
(条件式)
⇔ 5log105・5log10X=7log107・7log10X
よって (35)log1035×(35)log10Xにlog10Xを代入する。
(35)log1035×(35)log10X=(35)log1035×(35)-(log107+log105)
=(35)log105+log107×(35)-(log107+log105)
=350
=1
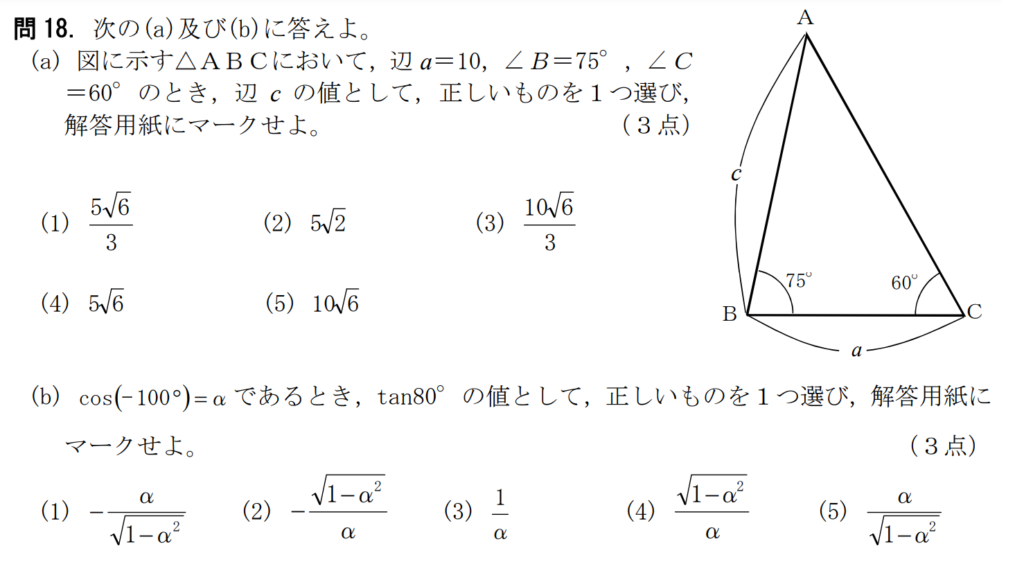
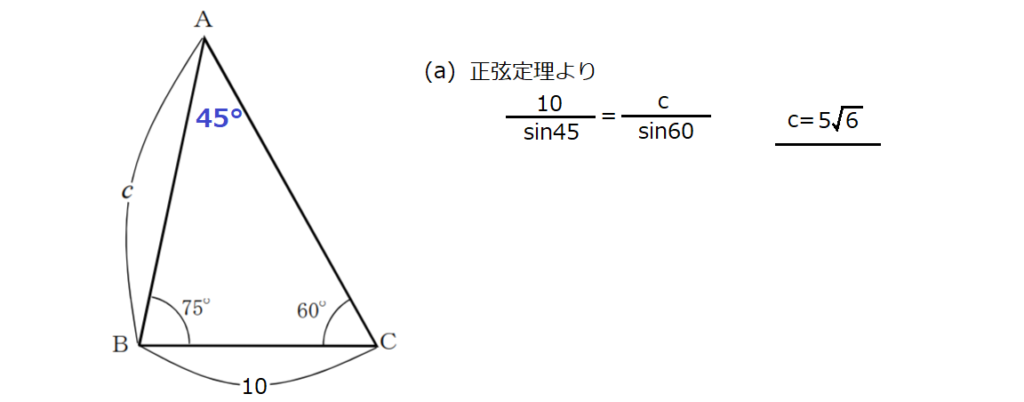
問18【数学:図形】答え(a)④.(b)②
航空大学校HPより引用
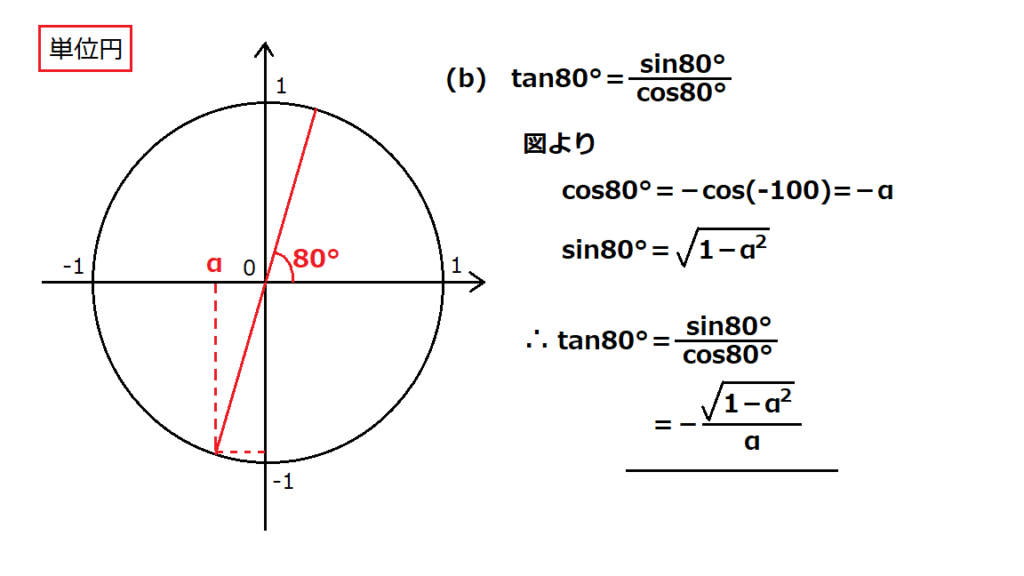
三角関数の基本は単位円。sinとcosの定義を使えばすぐに解ける。
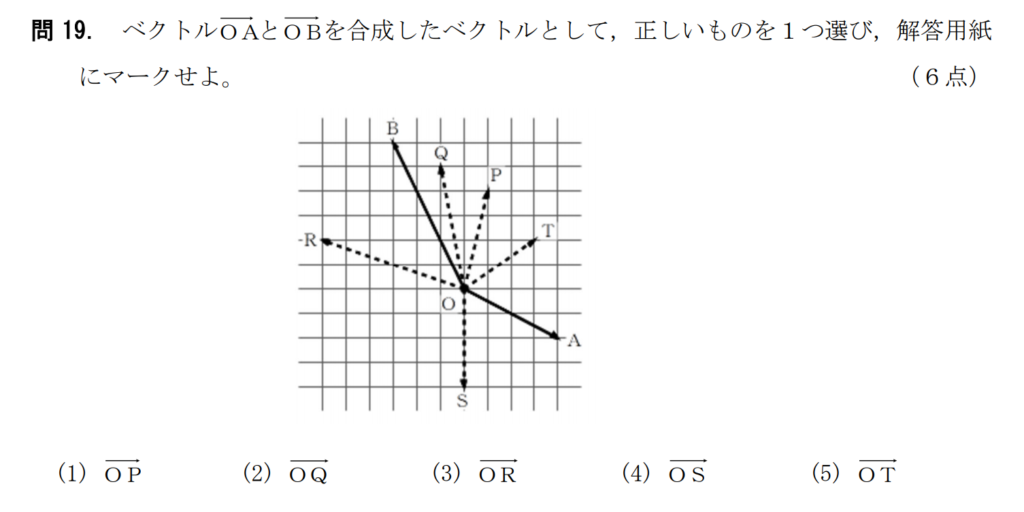
問19【数学:ベクトル】答え①
航空大学校HPより引用
3秒で解ける問題。(通称3秒問題)
ベクトルの概念が分かっているかを問う問題。
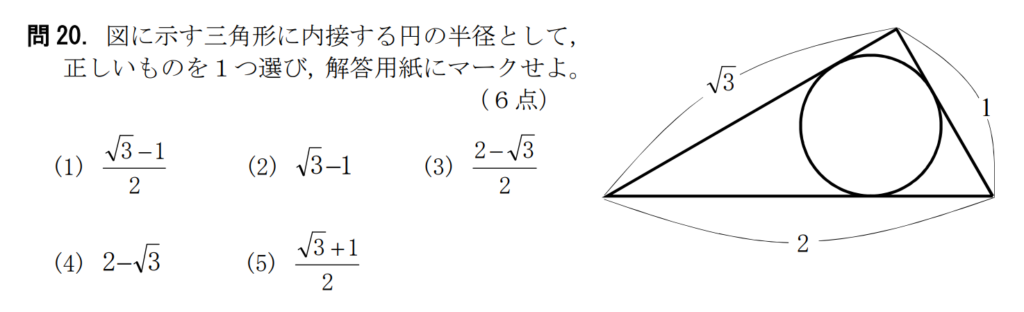
問20【数学:図形】答え①
航空大学校HPより引用
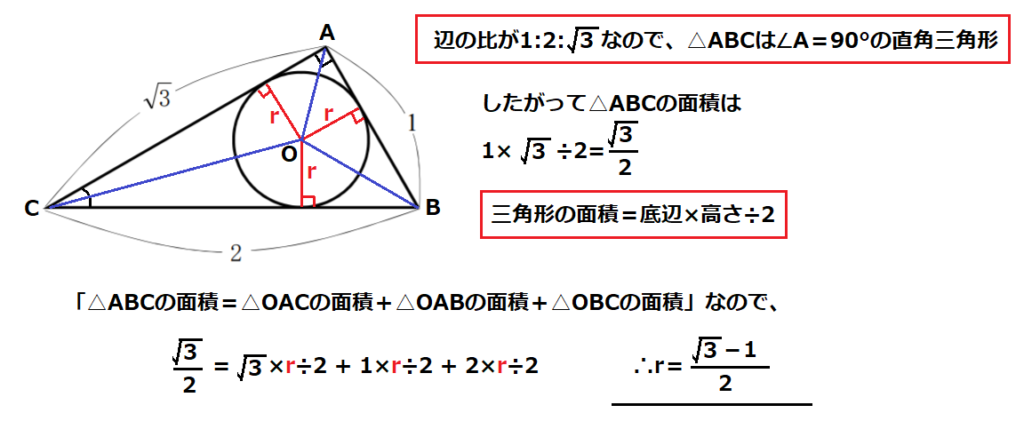
この問題は様々な解き方があると思うが、1番簡単でシンプルな解き方をする。
三角形の面積に着目して解く。
問21【数学:三角関数】答え④
航空大学校HPより引用
sin(-4Θ)=-sin(4Θ)なので
元の式は sin(4Θ)+cos(6Θ)=0
⇔ sin(5Θ-Θ)+cos(5Θ+Θ)=0
⇔ sin5ΘcosΘ-cos5ΘsinΘ+cos5ΘcosΘ-sin5ΘsinΘ(←加法定理で展開)
⇔ sin5Θ(cosΘ-sinΘ)+cos5Θ(cosΘ-sinΘ)=0(←因数分解していく)
⇔ (cosΘ-sinΘ)(sin5Θ+cos5Θ)=0(←ここから三角関数の合成を行う)
⇔ √2cos(Θ+π/4)・√2sin(5Θ+π/4)=0
⇔ 2cos(Θ+π/4)・sin(5Θ+π/4)=0
⇔ cos(Θ+π/4)=0 または sin(5Θ+π/4)=0
(0≦Θ≦2π)
(1)cos(Θ+π/4)=0 の場合
(Θの範囲:π/4≦ Θ+π/4 ≦9π/4)
Θ+π/4=π/2、3π/2
⇔ Θ=π/4、5π/4 (2個)
(2)sin(5Θ+π/4)=0 の場合
(Θの範囲:π/4≦ 5Θ+π/4 ≦10π+π/4)
5Θ+π/4=π、2π、3π、4π、5π、6π、7π、8π、9π、10π
⇔ 5Θ=3π/4、7π/4、11π/4、15π/4、19π/4、23π/4、27π/4、31π/4、35π/4、39π/4
⇔ Θ=3π/20、7π/20、11π/20、15π/20(=3π/4)、19π/20、23π/20、27π/20、31π/20、35π/20(=7π/4)、39π/20 (10個)
(1)(2)を足すと解の個数は12個。
問22【数学:指数関数】答え①
航空大学校HPより引用
4x+4-x-22+x-22-x+2=0
⇔ 4x+4-x-22・2x-22・2-x+2=0
⇔ 4x+4-x-22(2x+2-x)+2=0 ・・・(※)のように式は変更できる。
2x+2-x=t ・・・①と置く。
そうすると相加平均・相乗平均の関係より 2x+2-x≧2√2x・2-x=2 (つまりt≧2)
①の両辺を2乗する。
(2x+2-x)2=t2
⇔ 4x+4-x+2=t2
⇔ 4x+4-x=t2-2 ・・・②
(※)の式に①②を式に代入する。
t2-2-4t+2=0
⇔ t2-4t=0
⇔ t(t-4)=0
t≧2 なので t=4 となる。
∴2x+2-x=4
両辺に2xをかけると
(2x)2+1=4・(2x)
⇔ (2x)2-4・(2x)+1=0
解の公式より
2x=2±√3
∴x=log2(2±√3)
問23【数学:微分】答え⑤
航空大学校HPより引用
y=x3上の点(1,1)における接線の傾きはy=x3を微分することで求まる。
y’=3x2にx=1を代入すると傾きは3となる。よって接線はy=3x-2 となる。
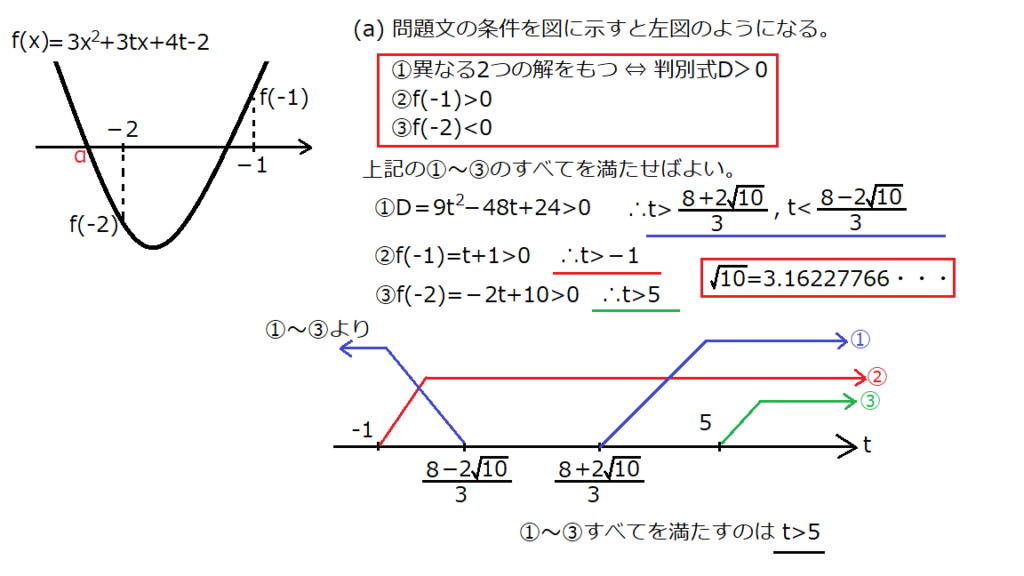
問24【数学:2次方程式】答え(a)③.(b)③
航空大学校HPより引用
問25【数学:極限】答え④
航空大学校HPより引用
この問題は局限値を求める問題で、局限値は数Ⅲの範囲。
しかし、やること自体は二次関数の積分であり数Ⅲをやってなくても感覚的に解くことは可能だと思う。