今回ですけども、飛行機の力学についてです。
飛行機は急には曲がれません。
曲がると決めて旋回を始めて90°変針した時にどれくらいの旋回半径となるのでしょうか。
また、飛行機の旋回半径はどのような式で表されるのでしょうか？
導いてみました。また、飛行機特有の速度の単位knot(ノット)に合わせた使い勝手の良い単位に変換してみました。
旋回半径はずっと使うので覚えておいて損はないです。
旋回半径の計算式
さて、この状態から旋回半径を出していきます。
旋回半径をRとしています。ここではRを出すのが目標です。
力学なので力を書き入れていきます。
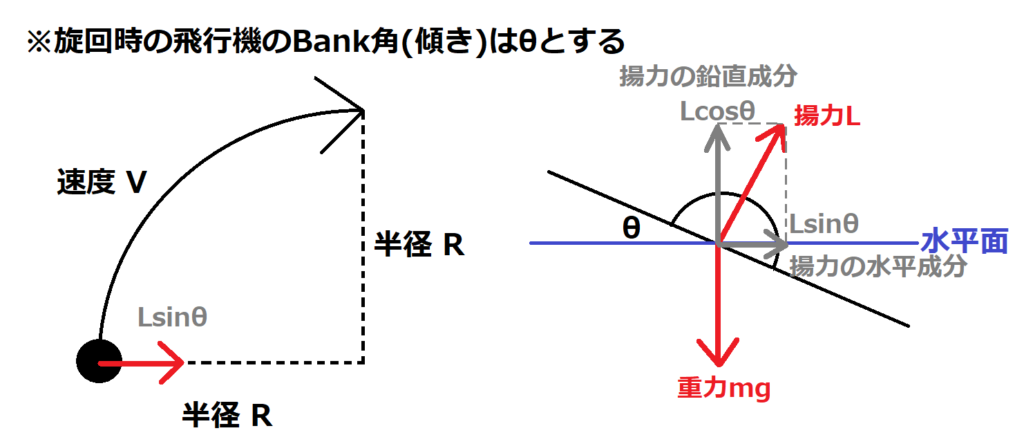
まず、飛行機が旋回するのを後ろから見た上記の図2から力を書き込んだ方が分かりやすいかもしれません。
飛行機に働く力はこのような力になります。
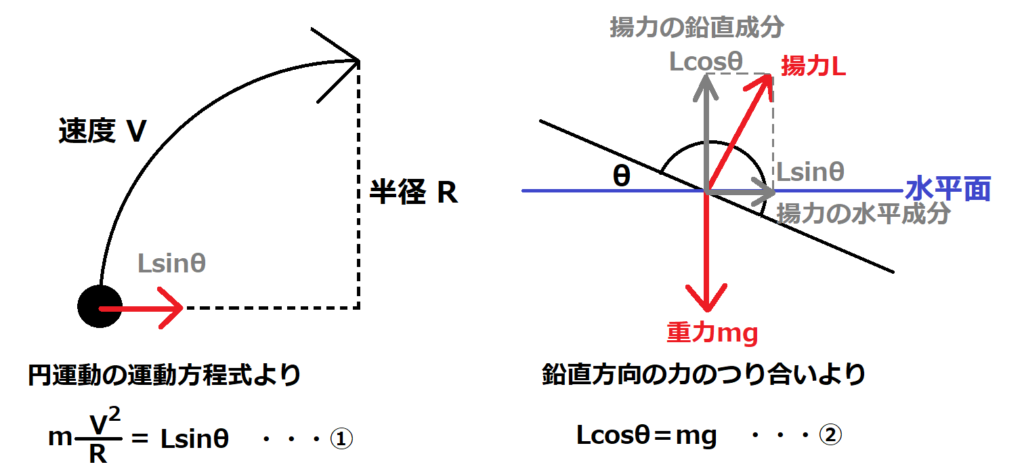
それぞれの図で立式してみます。
ここで、式の①と②から揚力Lを消します。
旋回半径の式が出ました。
ここで重要なのは旋回時の飛行機の傾きθが一定であれば、旋回半径Rは速度の2乗に比例するということです。
つまり、いつも同じBankで旋回するとすれば、飛行機の速度が決まれば旋回半径は決まるということです。
飛行機用の式に単位を変換する
導いた式のままでは少し使い勝手が悪いです。
式の中の重力加速度gは9.8m/s2です。また、速度の単位は[m/s]です。
飛行機の速度の単位はノット[knot]なのでそれに合わせた式にするとより便利です。
ちなみにノット[knot]という単位ですが、1knotは1時間に1ノーティカルマイル[NM]進むという意味です。
ノーティカルマイルは海里と呼ぶこともあり、1NM[海里]は1,852mです。
人間の歩く速さは大体時速4キロくらいですから、人間の歩く速さをノットに直すと約2ノットでしょうか。
飛行機の地上走行は大型機で20~30ノットくらいです。
話がそれましたが、単位を手直しします。
速度をknotで考える場合、重力加速度の単位が重力加速度が[m/s2]では都合が悪いです。
よって、9.8[m/s2]の単位を[knot/h2]に直しましょう。
9.8[m/s2]=9.8÷1852[NM/s2]
=9.8÷1852×36002[NM/h2]
=68579[NM/h2]
したがって、V[knot]で飛行している旋回半径[NM]は以下の式で表すことができます。
これは覚えておいて損はないと思います。ずっと使います。
重力加速度の単位変換まとめ
飛行機の世界では速度の単位はkt、高度についてはftを使うのでそれらに合わせた重力加速度をまとめておきます。
通常物理ではg=9.8m/s2が使われる。
上記からNM、hでのgは以下の通りです。
g=68579[NM/h2]
また、mをftに換算すると以下の通りとなります。(1m=3.281ft)
g=9.8×3.28≒32[ft/s2]
状況に合った単位を使うと良いと思います。
旋回と荷重倍数と失速速度の関係についてはこちらの記事で書いています。
[…] 【口述対策備忘録】飛行機の旋回半径！数式で理解する航空力学 […]