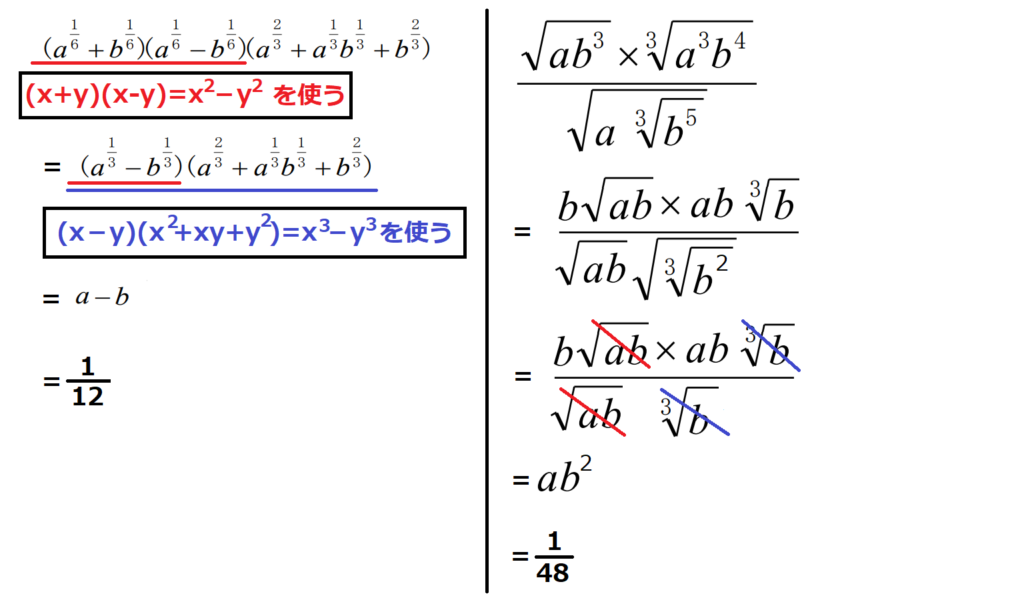航空大学校過去問解説です。
他の年度の過去問解説もありますのでブログの「航空大学校過去問解説」からチェックしてみてください。
毎年同じような問題なので傾向と対策は立てやすいかと思います。
定員が増えてからは1次試験の倍率は3倍程度です。
でも、ただ解くだけではなく、できるだけ最短の解き方をしています。
僕の解説のように解けば余った時間を他の問題に回すことができると思います。
目次
問1【時事問題】答え③
航空大学校HPより引用
(ア)「満18歳以上」なので誤り
(イ)正しい
(ウ)裁判員は6人。それに「民事事件」ではない。誤り。
問2【時事問題】答え①
航空大学校HPより引用
(ア)2016年ノーベル文学賞を受賞した。よって誤り。
(イ)「離脱」が上回った。よって誤り。
(ウ)令状が無ければ行うことはできない「強制捜査」にあたるとの見解を示した。よって誤り。
問3【社会:法律系】答え⑤
航空大学校HPより引用
問4【社会:航空知識系】答え③
航空大学校HPより引用
問5【地学:気象】答え⑤
航空大学校HPより引用
問6【化学:気象】答え②
航空大学校HPより引用
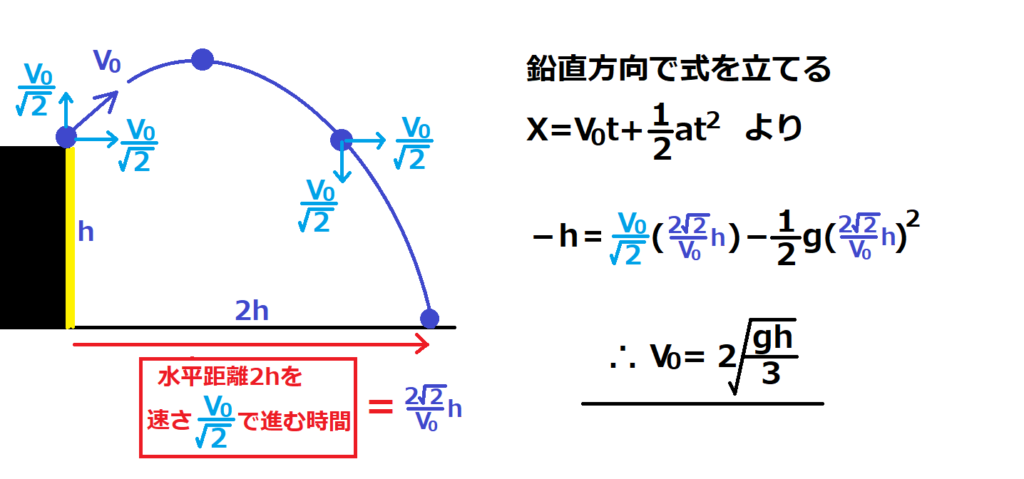
問7【物理:等加速度直線運動】答え(a)③.(b)⑤
航空大学校HPより引用
この問題は等加速度直線運動の式を立てて計算しても解けるけど、計算したら負け。
問8【物理:等加速度直線運動】答え⑤
航空大学校HPより引用
問9【物理:比熱】答え④
航空大学校HPより引用
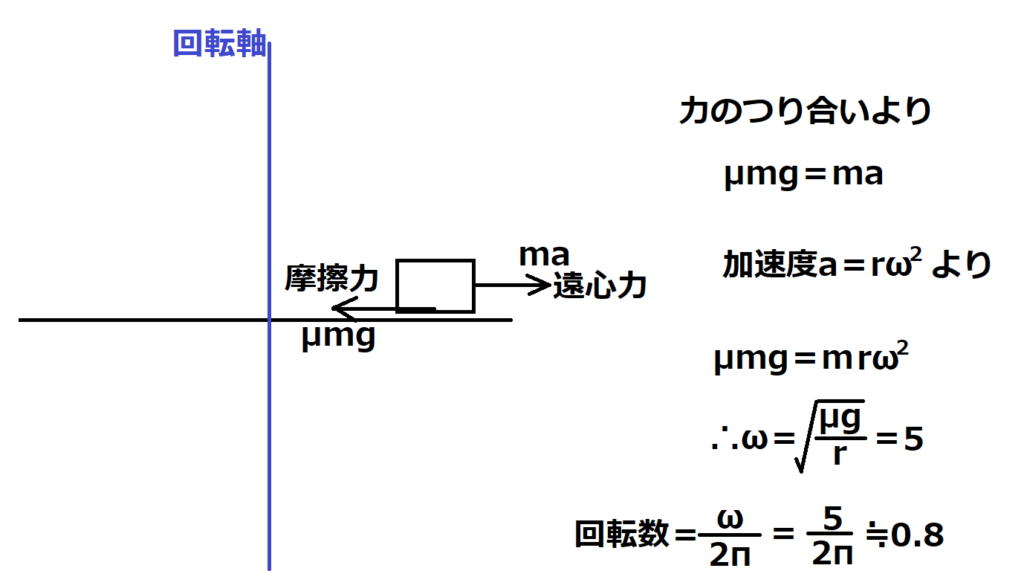
問10【物理:円運動】答え②
航空大学校HPより引用
※解法では遠心力(慣性力)を使ったが、慣性力を使わないのであれば円運動の運動方程式を使えば同じ式になる。
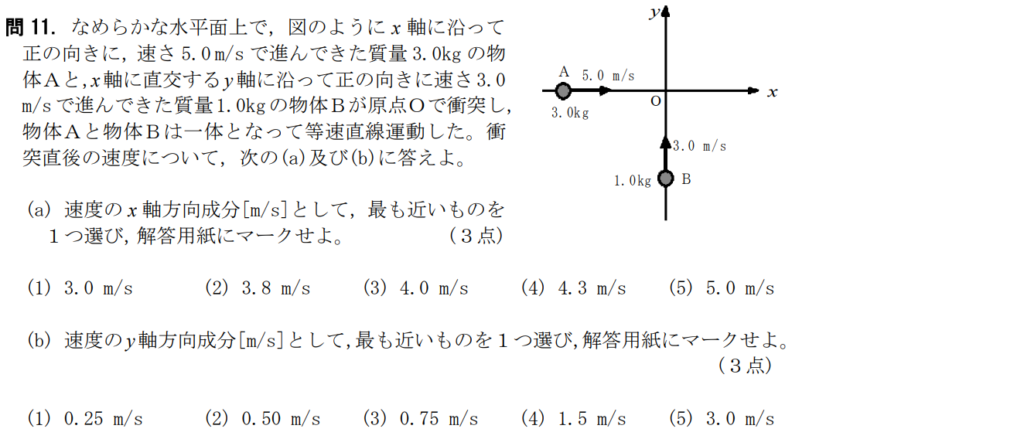
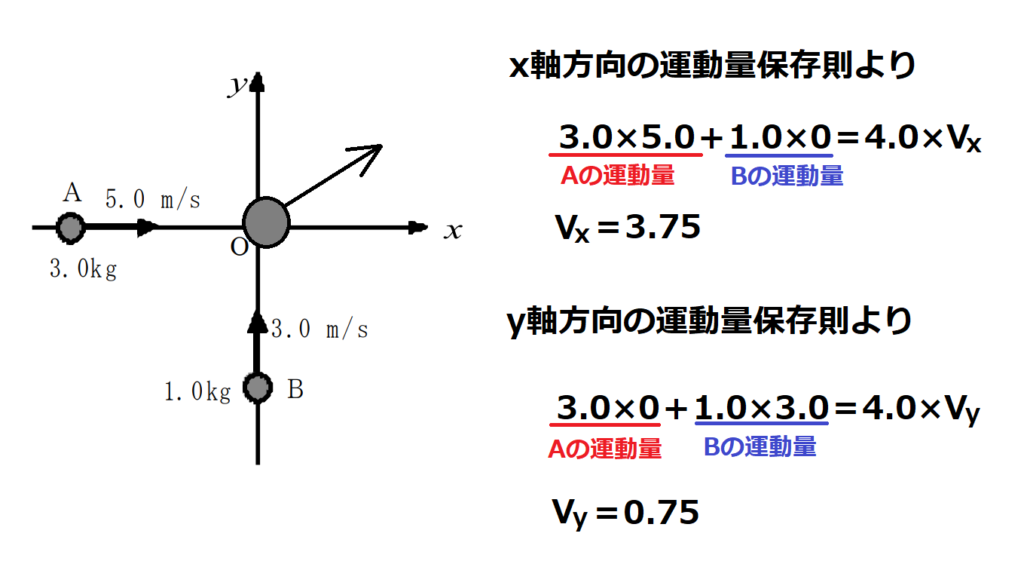
問11【物理:運動量保存則】答え(a)②.(b)③
航空大学校HPより引用
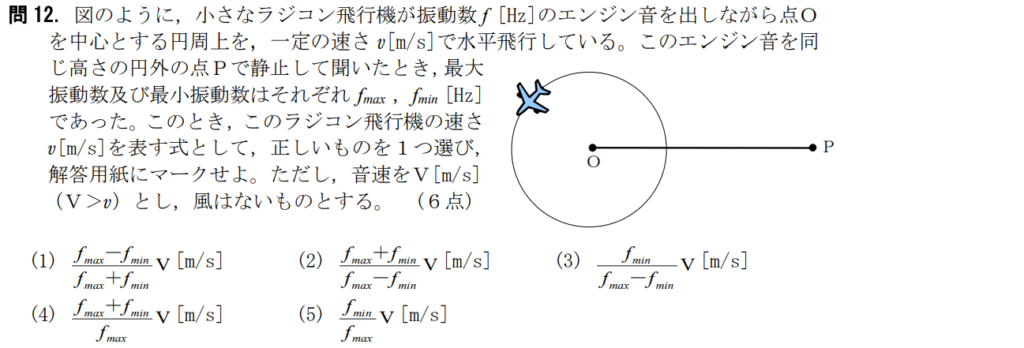
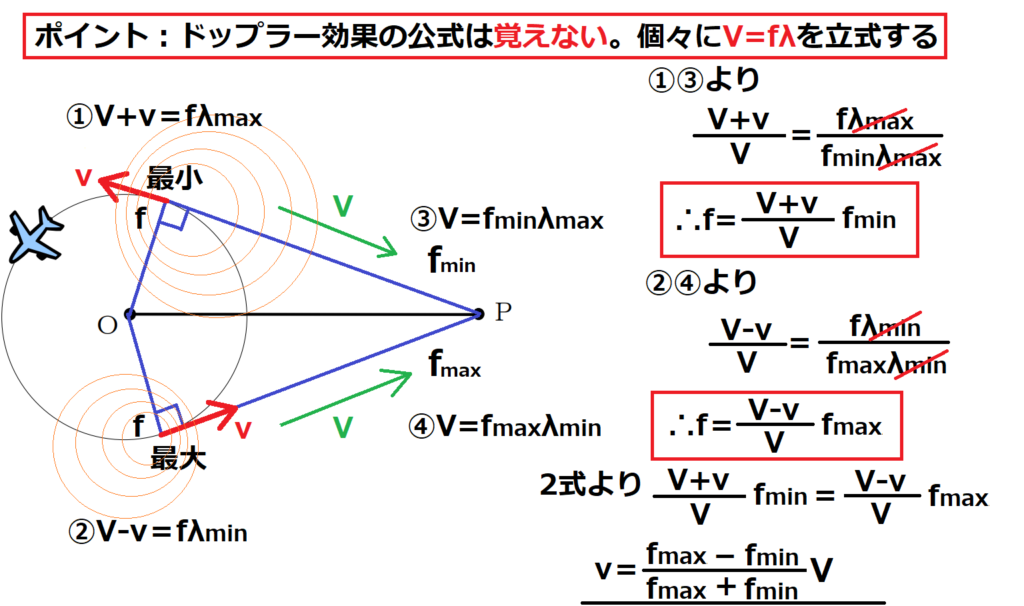
問12【物理:ドップラー効果】答え①
航空大学校HPより引用
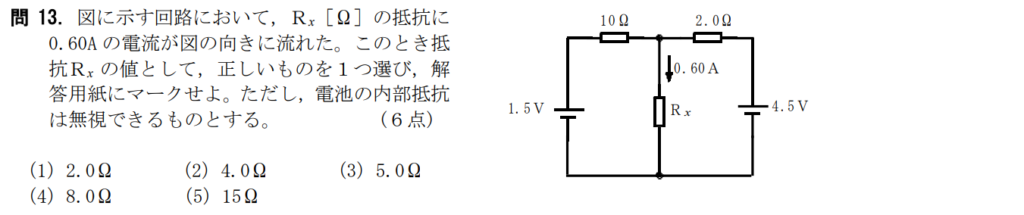
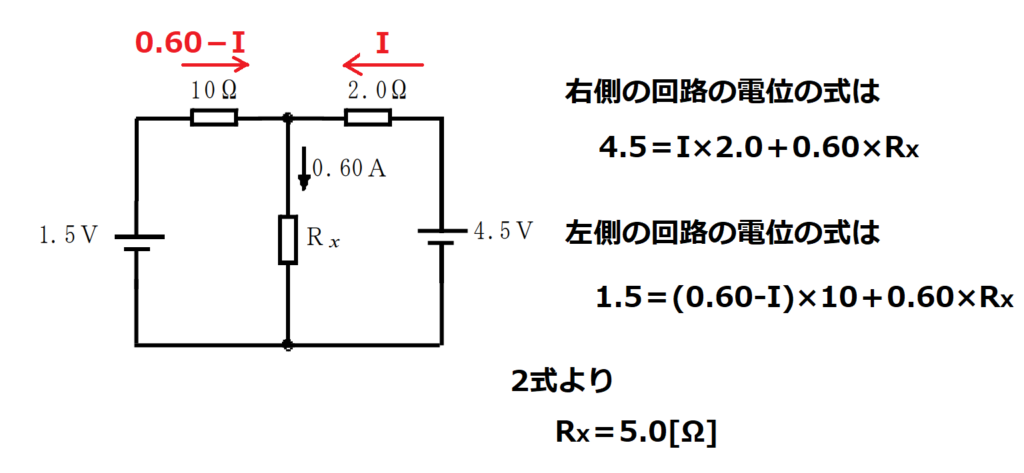
問13【物理:電気回路】答え③
航空大学校HPより引用
問14【物理:力学】答え④
航空大学校HPより引用
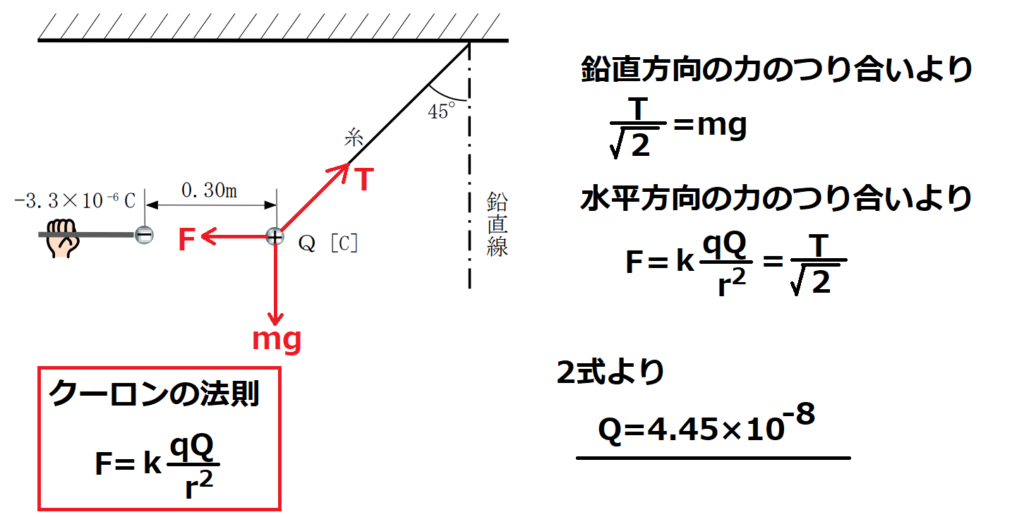
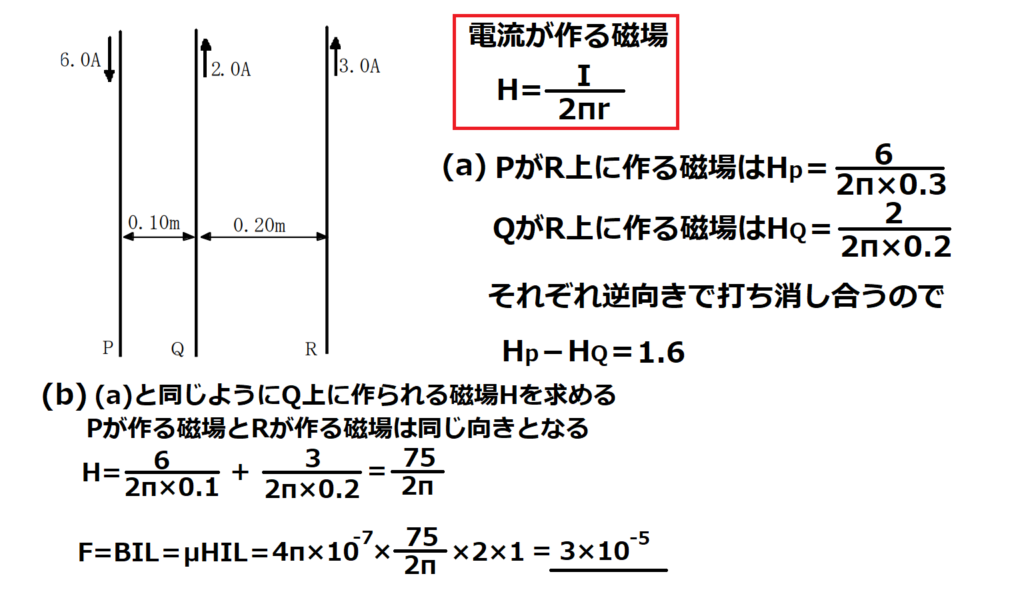
問15【物理:電磁気】答え(a)②.(b)⑤
航空大学校HPより引用
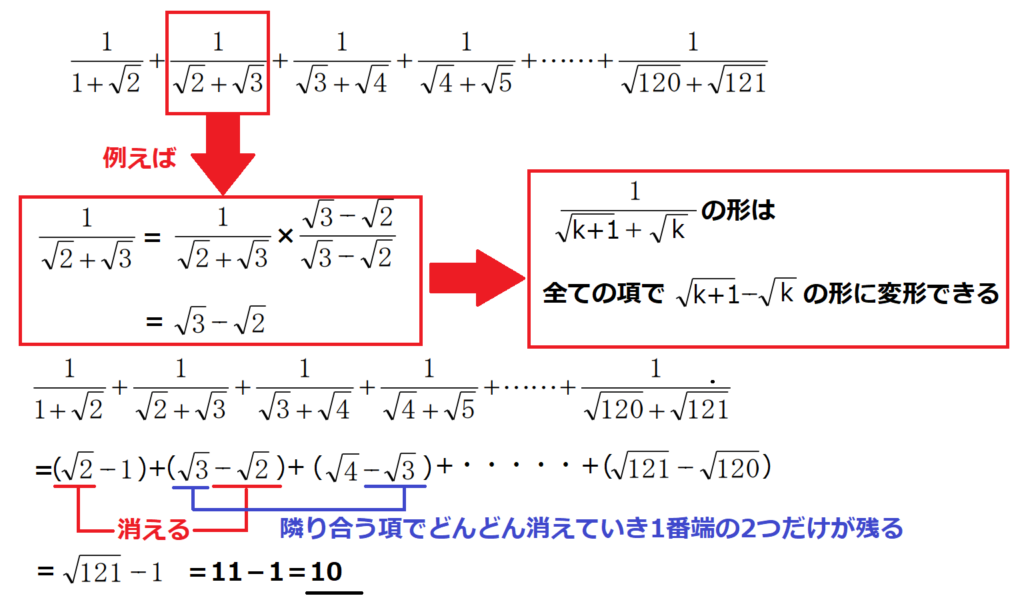
問16【数学:数列】答え③
航空大学校HPより引用
典型的な問題。
問17【数学:2次関数】答え⑤
航空大学校HPより引用
問18【数学:図形】答え(a)④.(b)②
航空大学校HPより引用
(a)余弦定理を使うだけの簡単な問題。
BD2=AB2+DA2-2AB×DA×cos∠A=9+25-30cos120=49
よってBD=7
(b)一般的な解法はまず余弦定理でcos∠Cを出してそれをsin∠Cに直す。
そのsin∠Cを使って三角形BDCの面積を出して、最終的に△ABDと△BDCの面積を足す。
が、僕はそれは面倒なのでやらない。
ヘロンの公式を使って三角形BDCの面積を出す。
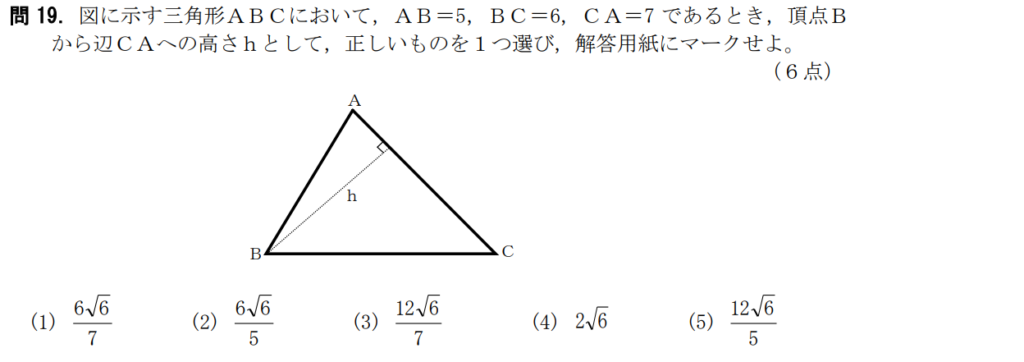
問19【数学:図形】答え③
航空大学校HPより引用
一般的な解法はまず余弦定理でcos∠Bを出してそれをsin∠Bに直す。
そのsin∠Bを使って三角形ABCの面積を出して、最終的に「面積=AC×h÷2」でhを求める。
が、僕はそれは面倒なのでやらない。
ヘロンの公式を使って三角形の面積を出す。
問20【数学:三角関数】答え④
航空大学校HPより引用
三角関数の計算問題。
三角関数の計算問題のポイントはsin2θ+cos2θ=1をうまく使うこと。
sin3θ-cos3θ=(sinθ-cosθ)(sin2θ+sinθcosθ+cos2θ)
=(sinθ-cosθ)(1+sinθcosθ)・・・(※)
sinθ-cosθ=a の両辺を2乗すると
sin2θ-2sinθcosθ+cos2θ=a2
∴sinθcosθ=(1-a2)/2
従って(※)の続き
=a×{1+(1-a2)/2}
=a(3-a2)/2
問21【数学:微分】答え①
航空大学校HPより引用
ただの計算問題。
微分して f'(x)=3x2+2ax+b
x=-1,3で極大・極小値を取るのでx=-1,3のときにf'(x)=0になる。
f'(x)=3x2+2ax+b=3(x+1)(x-3)
∴a=-3, b=-9
f(x)=x3-3x2-9x-2 となる。
後は計算するだけ
f(3)-f(-1)=-32
問22【数学:対数の計算】答え①
航空大学校HPより引用
一目みて答えは9。
9を代入すると成り立つのが暗算で確認できる。
ちゃんとやるなら
式をlog3x(x-8)=log332
に変形して
x(x-8)=9なので
x2-8x-9=0
(x-9)(x+1)=0
x>0なのでx=9
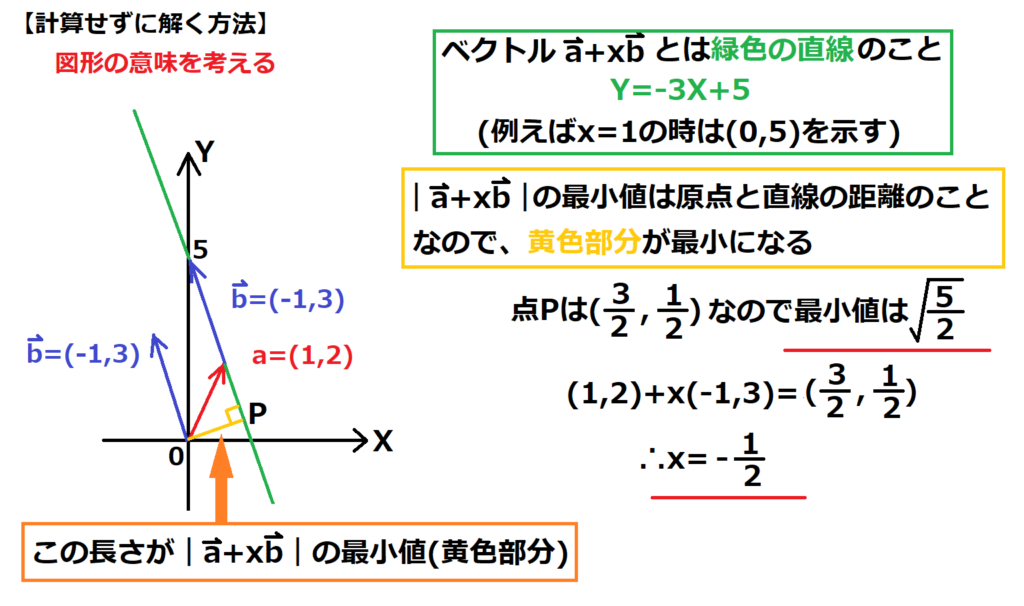
問23【数学:ベクトル】答え①
航空大学校HPより引用
問24【数学:指数の計算】答え(a)④.(b)④
航空大学校HPより引用
ただの計算問題。嫌がらせにしか見えない。
問25【数学:微分積分】答え①
航空大学校HPより引用
難しいように見えて簡単。
両辺をxで微分する。
xf'(x)+f(x)=12x3-12x+f(x)
両辺のf(x)が消えるのでf'(x)=12x2-12となる。
これを積分すると
f(x)=4x3-12x+C(Cは積分定数)・・・①(この時点で(1)が答えなのでCを求めなくてもOK)
ここで、問題文の式にx=2を代入すると
2f(2)=3×24-6×22+2
∴f(2)=13
①の式にx=2を代入する。
f(2)=4×23-12×2+C=13
∴C=5
求める式はf(x)=4x3-12x+5