航空大学校過去問【2019年度(H31)　総合Ⅱ　解答・解説】

航空大学校の過去問解説です。

他の年度の過去問解説もありますのでブログのカテゴリーの中の「航空大学校過去問解説」からチェックしてみてください。

毎年同じような問題なので傾向と対策は立てやすいかと思います。

定員が増えてからは１次試験の倍率は３倍程度です。

ただ解くだけではなく、できるだけ最短の解き方をしています。

僕の解説のように解けば余った時間を他の問題に回すことができると思います。

2026年から出題範囲が変わるようなのでまず以下の記事をチェックしてみてください。
↓↓↓↓↓↓↓↓↓↓↓↓

物理が苦手な方はこちらの記事へ。

問１【時事問題：航空知識系】答え①

解説

成田国際空港は滑走路が2本あって、4000mと2500m。

関西国際空港も滑走路が2本あって4000mと3500m。

ちなみに中部国際空港の滑走路は1本で長さは3500m。

那覇空港は2020年3月に2本目の滑走路が完成した。

問２【時事問題：知識系】答え④

解説

(ア)クールジャパンの「クール」はかっこいいという意味。日本の文化を世界に発信して外国の日本ファンを取り込む戦略のこと。
(イ)正しい
(ウ)「５年以上」ではなく「１０年以上」
(エ)「毎週金曜」ではなく「月の最終金曜」

問３【社会：法律系】答え①

問４【社会：知識系】答え④

問５【地学：気象】答え⑤

問６【化学：気体】答え④

問７【物理：波動】答え(a)①.(b)①

(a)については知識問題。

(b)について、

波の基本式：v＝f λに数値を代入するだけの簡単な計算問題。

物理法則の式は単位が決まってて、基本的には長さは[m]、速度は[m/s]、振動数は[Hz]。

３３１.５＋０.６×１５＝２００００× λ

∴λ＝０.０１７[m]　(１.７cm)

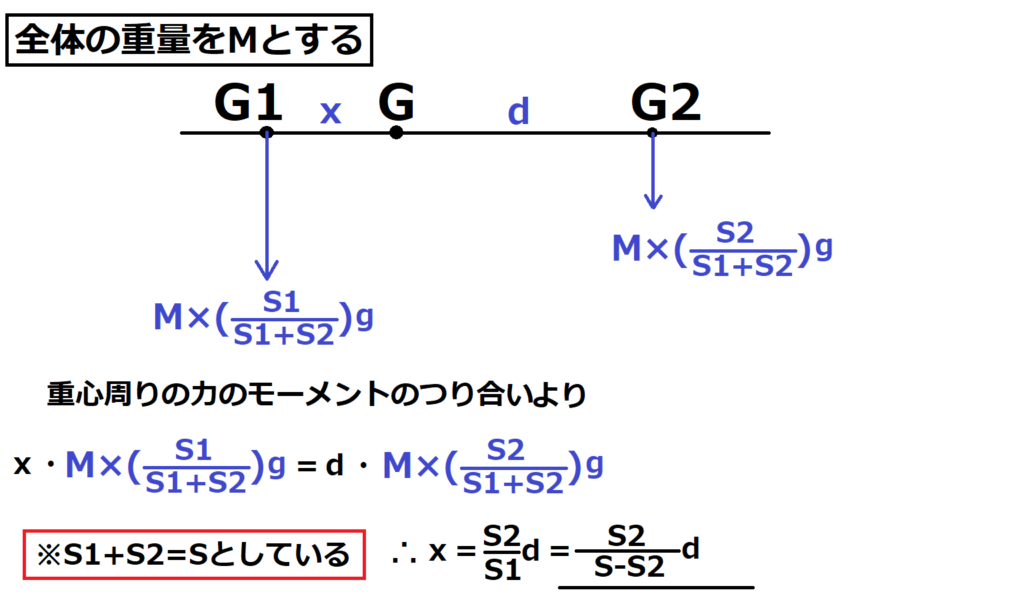
問８【物理：力のモーメント】答え③

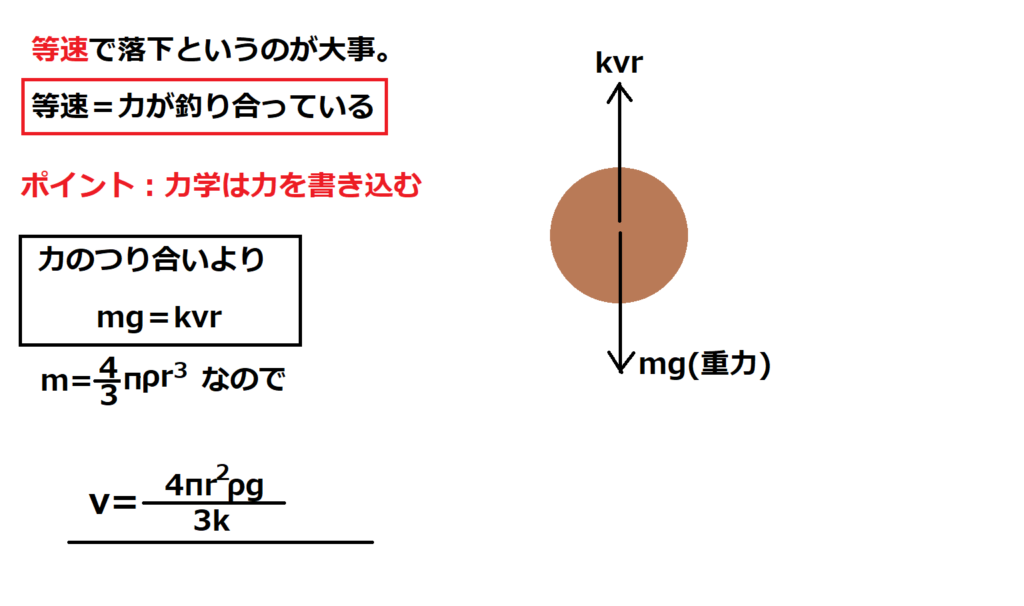
問９【物理：力のつり合い】答え①

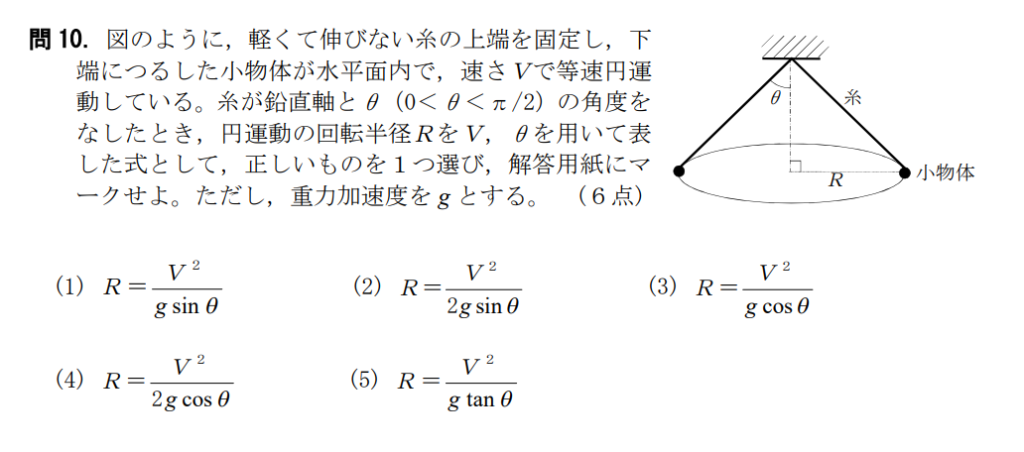
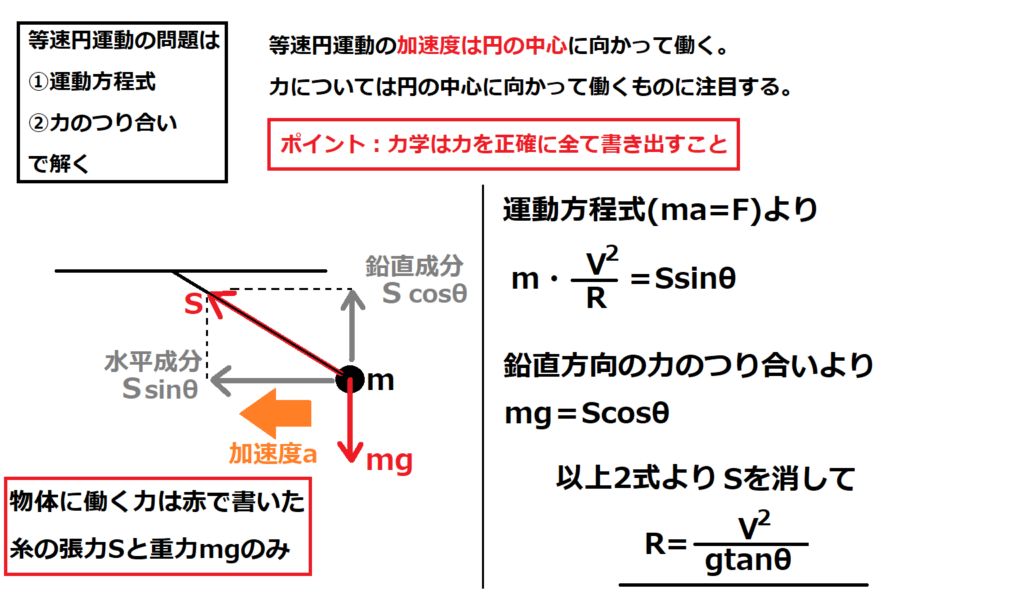
問１０【物理：等速円運動】答え⑤

ちなみに等速円運動のときの加速度aは様々な形がある。今回はa=V²/Rの形を使ったがどの形でも自由自在に使えるようにしておくことが大事。

a=rω² =V²/R
=Vω

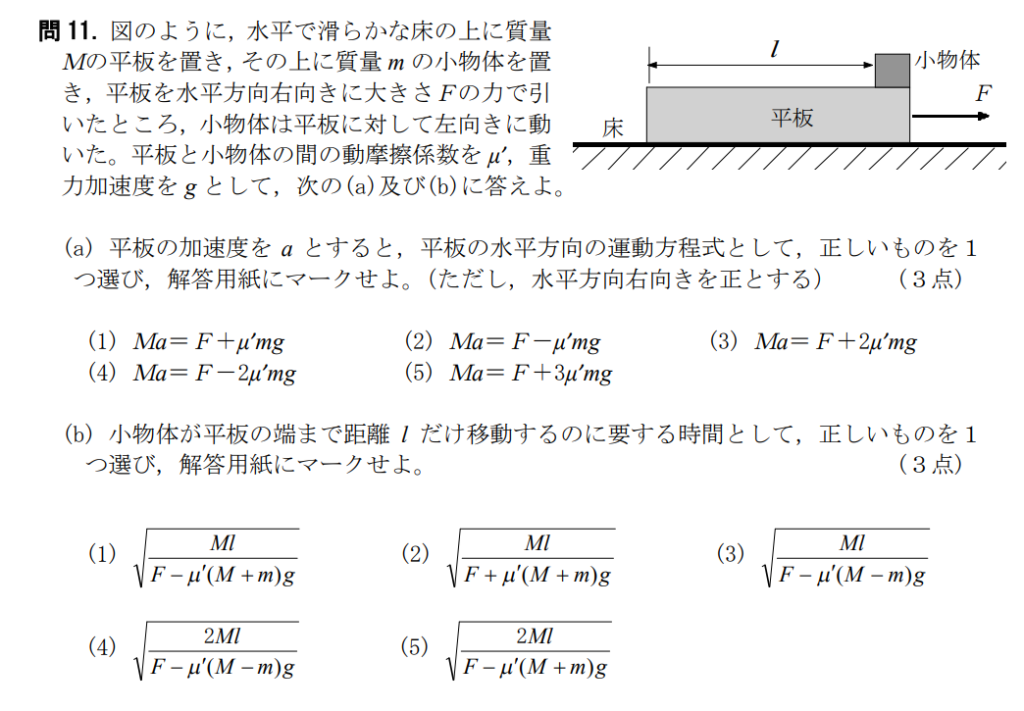
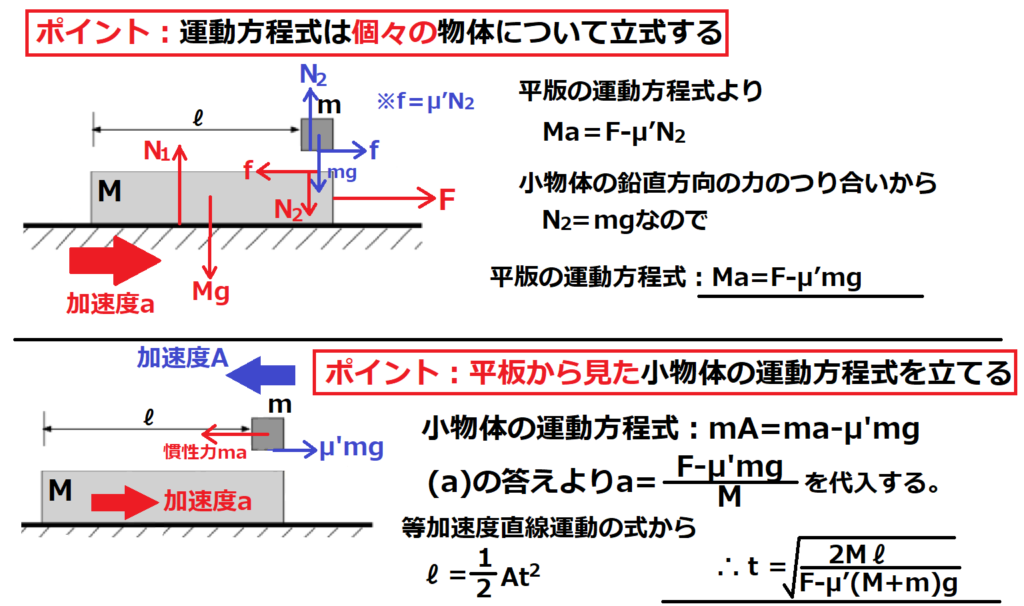
問１１【物理：運動方程式】答え(a)②.(b)⑤

これも公式に当てはめるだけの簡単な問題だが、慣性力についてよく理解していないと混乱する可能性あり。

差がつくであろう問題です。

問１２【物理：等加速度直線運動】答え②

この問題はそんなに難しくないが、解き方によって時間差が出る問題。

僕の解き方だと一瞬で解けるのでぜひ覚えてもらいたい。

ごりごり数式を立てて計算した人は時間ロス。

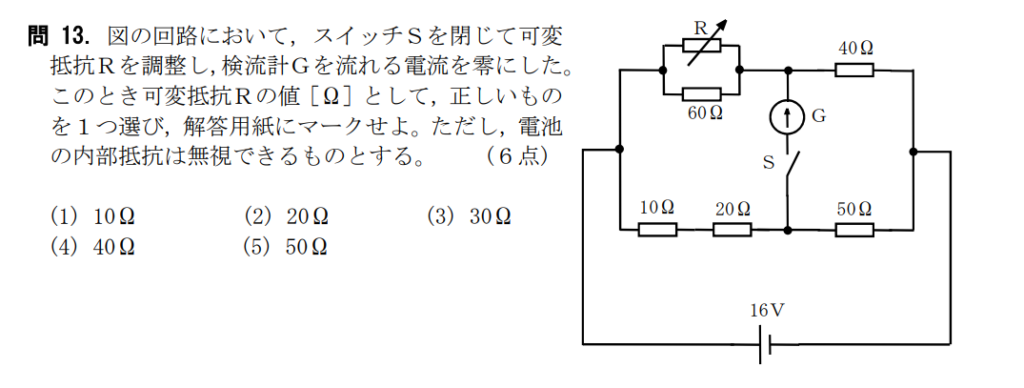
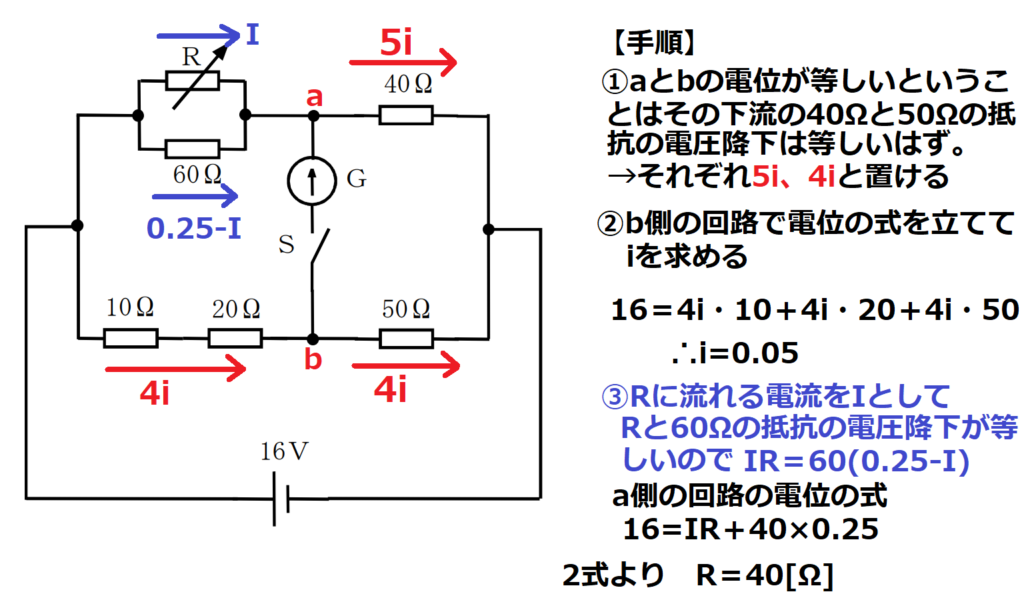
問１３【物理：電気回路】答え④

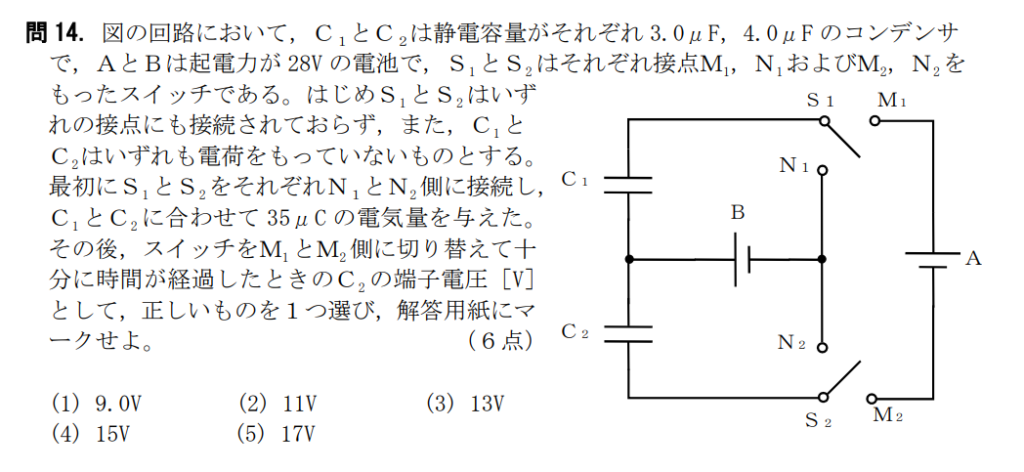
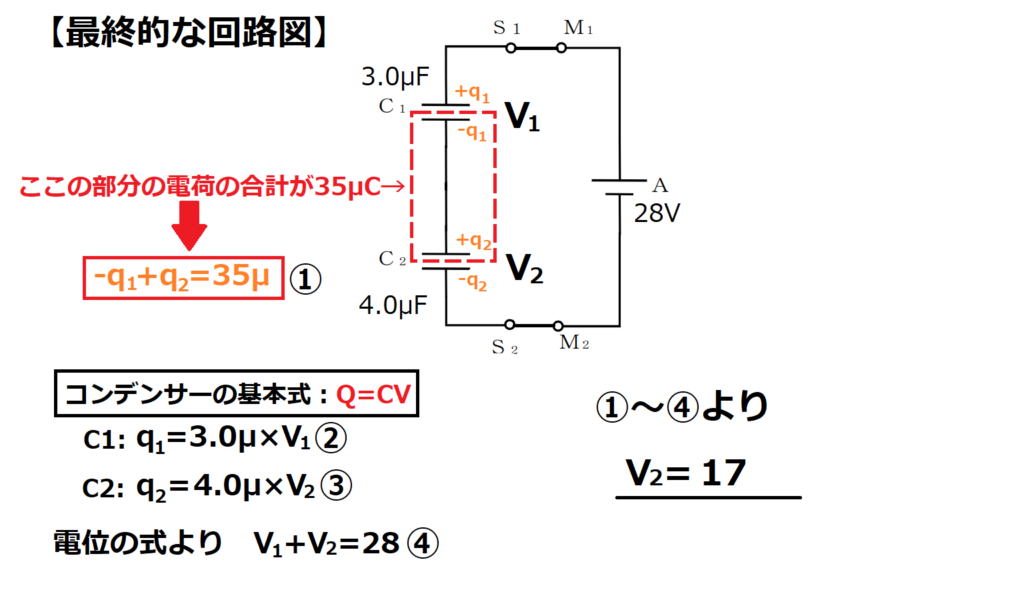
問１４【物理：電気回路】答え⑤

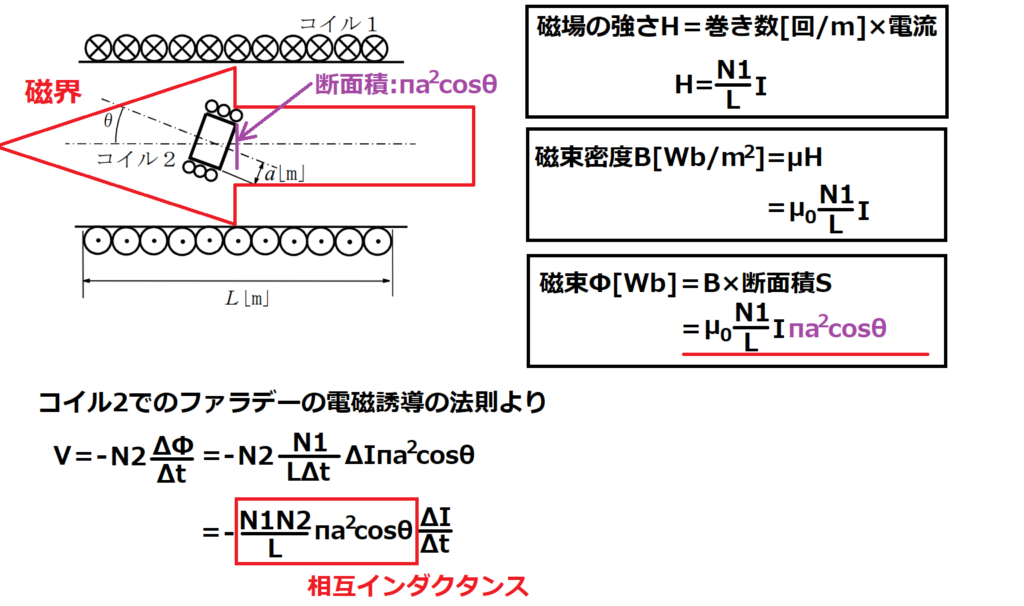
問１５【物理：電磁気】答え(a)⑤.(b)③

問１６【数学：２進法】答え④

【解き方は機械的】

９３＝１・２^６＋０・２^５＋１・２^４＋１・２^３＋１・２^２＋０・２^１＋１・２^０

→よって１０１１１０１が答え

(参考)もし３進法なら

９３＝１・３^４＋０・３^３＋１・３^２＋１・３^１＋０・３^０

→１０１１０となる

問１７【数学：対称式】答え②

(x+y+z)^２＝x^２+y^２+z^２+２(xy+yz+zx)なので

x^２+y^２+z^２＝－２(xy+yz+zx)－(x+y+z)^２＝１４・・・①

x^３+y^３+z^３－３xyz＝(x+y+z)(x^２+y^２+z^２－xy-yz-zx)という因数分解の有名な形を利用して

x^３+y^３+z^３＝１８・・・②

(x^２+y^２+z^２)^２＝x^４+y^４+z^４+２(x^２y^２+y^２z^２+z^２x^２)なので

x^２y^２+y^２z^２+z^２x^２の値が分かればx^４+y^４+z^４を求められそう。

よって

(xy+yz+zx)^２＝x^２y^２+y^２z^２+z^２x^２＋２xyz(x+y+z)

∴x^２y^２+y^２z^２+z^２x^２＝(xy+yz+zx)^２－２xyz(x+y+z)＝４９

従って

x^４+y^４+z^４＝(x^２+y^２+z^２)^２－２(x^２y^２+y^２z^２+z^２x^２)＝１４^２－２・４９＝９８・・・③

①～③より答えは１３０

問１８【数学：ベクトル】答え(a)③.(b)⑤

問１９【数学：方程式】答え①

方針としては文字を１つに統一する。

問２０【数学：三角関数】答え②

三角関数の5倍角の定理の問題。覚えている人はもしかしたらいるかも。

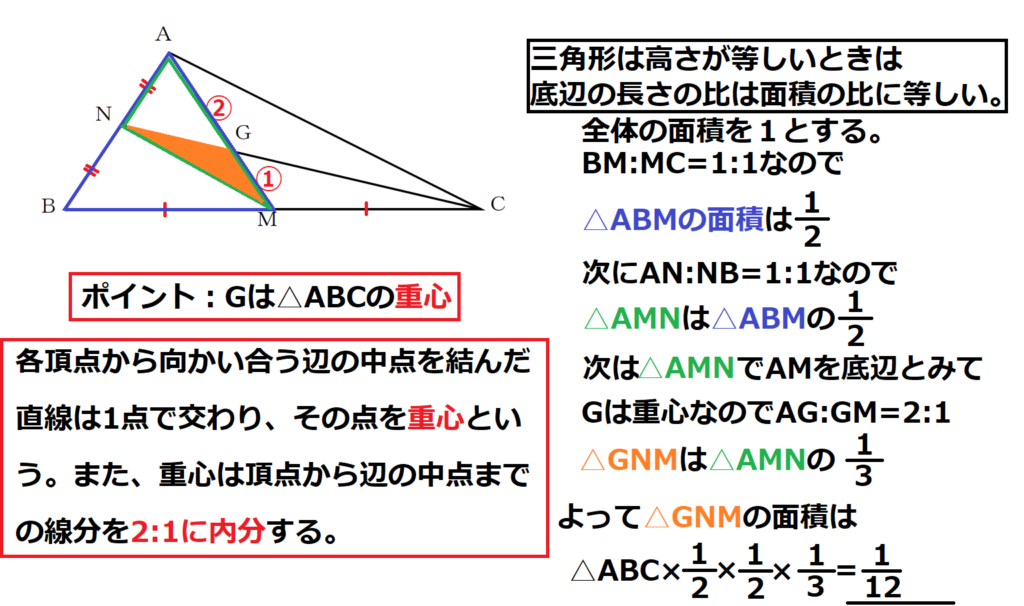
問２１【数学：図形】答え③

問２２【数学：２次方程式】答え③

問２３【数学：不等式】答え①

順に代入していけば絶対解ける。

log_y81=log_y3⁴=4log_y3なので

元の式を変形すると

2+log_√y3<4log_y3+2log_y(1-x/2)

(1)2+log_√23<4log₂3+2log₂1

⇔2+log_√23<4log₂3

⇔2+2log₂3<4log₂3

⇔1<log₂3——> 〇

(2)2+log_√43<4log₄3+2log₄1

⇔2+log_√43<4log₄3

⇔2+log₂3<2log₂3

⇔2<log₂3——> ×

(3)2+log_√23<4log₂3+2log₂(1/2)

⇔2+2log₂3<4log₂3－2

⇔4<2log₂3

⇔2<log₂3——> ×

(4)2+log_√33<4log₃3+2log₃(1/2)

⇔2+2<4+2log₃(1/2)

⇔0<log₃(1/2)

⇔0>log₃2——> ×

(5)2+log_√43<4log₄3+2log₄(1/2)

⇔2+log_√43<4log₄3+2log₄(1/2)

⇔2+log₂3<4log₄3－2log₄2

⇔2+log₂3<2log₂3－1

⇔3<log₂3——> ×

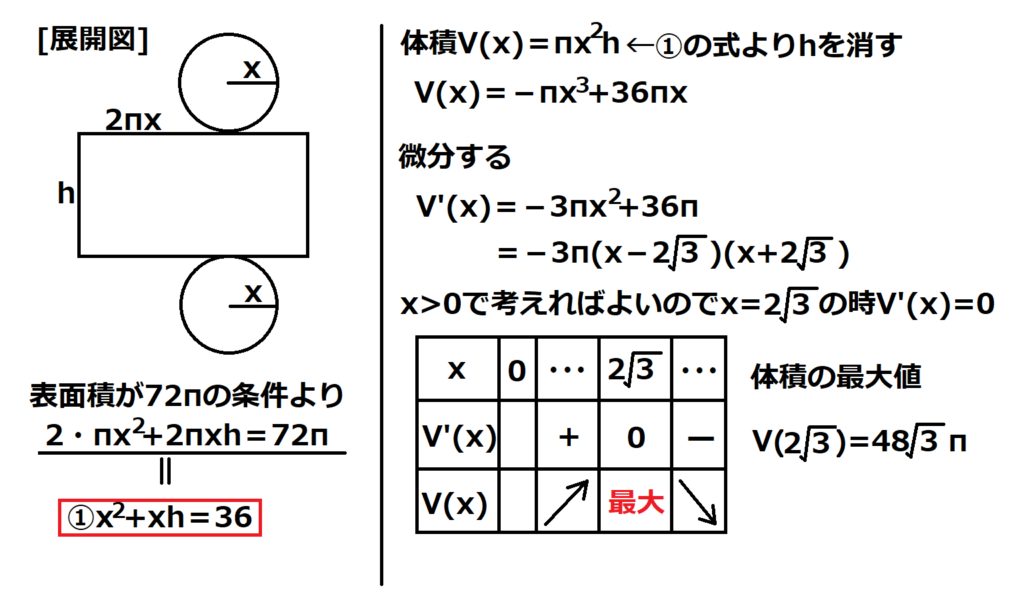
問２４【数学：微分】答え(a)③.(b)⑤

簡単な微分の計算問題。典型的でひねりはない。

半径をx、直円柱の高さをhと置き、展開図を書く。

問２５【数学：積分】答え②

式を展開していって積分計算すれば絶対解けるただの計算問題である。定積分計算が間違わずにできるかどうか、そこだけである。

一見4次式の積分で嫌がらせのように見えるかもしれないが、これはやりようによっては瞬殺問題。

積分する関数の変形を工夫する。

定積分で最終的に1と2を代入するので最後に(x－1)もしくは(x－2)の項が残っていれば計算する上でかなり有利。

よって(x－2)が残るように変更していく。

{(x-1)(x-2)}²

＝(x-1)²(x-2)²

={(x-2)+1}²(x-2)²

＝{(x-2)²+2(x-2)+1}(x-2)²

=(x-2)⁴+2(x-2)³+(x-2)²

こういうところで時間を節約できると差がつきます。

「数強塾」オンライン数学克服塾〈プロ講師〉

航空大学校過去問【2019年度(H31) 総合Ⅱ 解答・解説】